题目内容
14.解方程组$\left\{\begin{array}{l}{3x+2y=1}\\{2x-3y=5}\end{array}\right.$.分析 将方程①×3+②×2可求得x的值,将x的值代入①可求得y.
解答 解:解方程组$\left\{\begin{array}{l}{3x+2y=1}&{①}\\{2x-3y=5}&{②}\end{array}\right.$,
①×3,得:9x+6y=3 ③,
②×2,得:4x-6y=10 ④,
③+④,得:13x=13,解得:x=1,
将x=1代入①,得:3+2y=1,解得:y=-1,
故方程组的解为:$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$.
点评 本题考查了解二元一次方程组:利用代入消元或加减消元把二元一次方程组转化为一元一次方程,解一元一次方程先求出一个未知数的值,然后把这个未知数的值代入原方程组中任一方程求出另一个未知数的值,这样就得到方程组的解.

练习册系列答案
相关题目
4.关于x的一元二次方程$\frac{1}{2}{x}^{2}$+3x+k=0有两个不相等的实数根,则k的取值范围是( )
| A. | k$<\frac{9}{2}$ | B. | k=$\frac{9}{4}$ | C. | k$≥\frac{9}{2}$ | D. | k$>\frac{9}{4}$ |
9.已知关于x的方程x4-ax2+1=0无实数根,则实数a的取值范围为( )
| A. | -2<a<2 | B. | a<0 | C. | -2<a<0 | D. | a<2 |
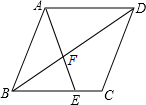 如图所示,在菱形ABCD中,E是BC上一点,且AE=AB,∠EAD=2∠BAE.求证:BE=AF.
如图所示,在菱形ABCD中,E是BC上一点,且AE=AB,∠EAD=2∠BAE.求证:BE=AF.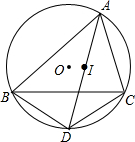 如图,已知△ABC内接于⊙O,点I是△ABC的内心,AI的延长线交BC于点E,交⊙O于点D.
如图,已知△ABC内接于⊙O,点I是△ABC的内心,AI的延长线交BC于点E,交⊙O于点D.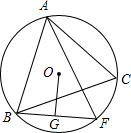 已知△ABC内接于⊙O,F是弧$\widehat{BC}$上一点,OG⊥BF于点G,且OG=$\frac{1}{2}$AC.证明:AF⊥BC.
已知△ABC内接于⊙O,F是弧$\widehat{BC}$上一点,OG⊥BF于点G,且OG=$\frac{1}{2}$AC.证明:AF⊥BC.