题目内容
1.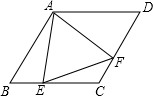 如图,在菱形ABCD中,∠B=60°,若AB=2,点E是BC边上一动点,∠EAF=60°,AF交CD于点F
如图,在菱形ABCD中,∠B=60°,若AB=2,点E是BC边上一动点,∠EAF=60°,AF交CD于点F(1)探究线段AE、AF的数量关系,并写出解答过程;
(2)当点E运动到什么位置时,△AEF的面积最小,最小面积是多少?
分析 (1)由△ABC是等边三角形,即可得AB=AC,求得∠ACF=∠B=60°,然后利用平行线与三角形外角的性质,可求得∠AEB=∠AFC,证得△AEB≌△AFC,即可得AE=AF,证得△AEF是等边三角形即可;
(3)由垂线段最短可知:当AE⊥BC时,AE有最小值,然后由特殊锐角三角函数值可求得AE的长,即可得出结果.
解答 解:(1)AE=AF,理由如下:
连接AC.如图所示:
∵四边形ABCD是菱形,
∴AB=BC,∵∠B=60°,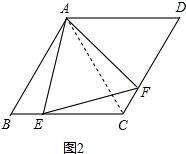 ∴△ABC是等边三角形,
∴△ABC是等边三角形,
∴AB=AC,∠ACB=60°.
∴∠B=∠ACF=60°.
∵AD∥BC,
∴∠AEB=∠EAD=∠EAF+∠FAD=60°+∠FAD,∠AFC=∠D+∠FAD=60°+∠FAD.
∴∠AEB=∠AFC.
在△ABE和△ACF中,
$\left\{\begin{array}{l}{∠B=∠ACF}&{\;}\\{∠AEB=∠AFC}&{\;}\\{AB=AC}&{\;}\end{array}\right.$,
∴△ABE≌△ACF(AAS).
∴AE=AF.
(3)由垂线段最短可知:当AE⊥BC时,AE有最小值.
∵AE=AF.∠EAF=60°,
∴△AEF是等边三角形.
∵AE⊥BC,∠B=60°,
∴AE=AB•sin60°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∴EF=$\sqrt{3}$,此时△AEF的面积=$\frac{1}{2}$×$\sqrt{3}$×$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{4}$;
当AE⊥BC时,△AEF的面积最小,最小面积是$\frac{3\sqrt{3}}{4}$.
点评 本题考查了菱形的性质、等边三角形的判定与性质、全等三角形的判定与性质、三角函数等知识;熟练掌握菱形的性质,证明三角形全等是解决问题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | -2<a<2 | B. | a<0 | C. | -2<a<0 | D. | a<2 |
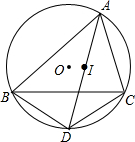 如图,已知△ABC内接于⊙O,点I是△ABC的内心,AI的延长线交BC于点E,交⊙O于点D.
如图,已知△ABC内接于⊙O,点I是△ABC的内心,AI的延长线交BC于点E,交⊙O于点D. 如图,△ABC中,O为外心,三条高AD、BE、CF交于点H,直线ED和AB交于点M,FD和AC交于点N.求证:OH⊥MN.
如图,△ABC中,O为外心,三条高AD、BE、CF交于点H,直线ED和AB交于点M,FD和AC交于点N.求证:OH⊥MN.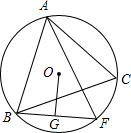 已知△ABC内接于⊙O,F是弧$\widehat{BC}$上一点,OG⊥BF于点G,且OG=$\frac{1}{2}$AC.证明:AF⊥BC.
已知△ABC内接于⊙O,F是弧$\widehat{BC}$上一点,OG⊥BF于点G,且OG=$\frac{1}{2}$AC.证明:AF⊥BC.