题目内容
17.如图1,已知抛物线y=-x2+bx+c经过点A(1,0),B(-3,0)两点,且与y轴交于点C.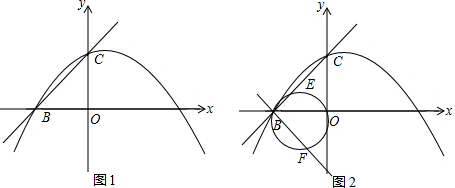
(1)求b,c的值;
(2)在第二象限的抛物线上,是否存在一点P,使得△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若不存在,请说明理由;
(3)如图2,点E为线段BC上一个动点(不与B,C重合),经过B,E,O三点的圆与过点B且垂直于BC的直线交于点F,当△OEF面积取得最小值时,求点E坐标.
分析 (1)将点A和点B的坐标代入抛物线y=-x2+b x+c得到关于b、c的方程组,然后解方程组即可;
(2)先利用待定系数法求出BC的解析式,设P点(x,-x2-2x+3)(-3<x<0),则D(x,x+3),则PD=-x2-3x,则利用S△BPC=S△PBD+S△CPD=$\frac{1}{2}$•3•(-x2-3x)得到S与x的二次函数关系式,然后利用二次函数的性质解决问题;
(3)根据圆周角定理得出OE=OF,∠EOF=90°,利用S△OEF=OE•OF=OE2,进而分析得出OE最小时,△OEF面积取得最小值,进而得出E点在BC的中点时,即可得出答案.
解答 解:(1)把A(1,0),B(-3,0)代入y=-x2+bx+c得$\left\{\begin{array}{l}{1+b+c=0}\\{-9-3b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-2}\\{c=3}\end{array}\right.$,.
所以抛物线的解析式为y=-x2-2x+3;
(2)存在.
如图1,作PD∥y轴交BC于D,
设直线BC的解析式为y=mx+n,
把B(-3,0),C(0,3)代入得$\left\{\begin{array}{l}{-3m+n=0}\\{n=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=1}\\{n=3}\end{array}\right.$.
故直线BC的解析式为y=x+3,
设P点(x,-x2-2x+3)(-3<x<0),则D(x,x+3),
∴PD=-x2-2x+3-(x+3)=-x2-3x,
∴S△BPC=S△PBD+S△CPD
=$\frac{1}{2}$•3•(-x2-3x)
=-$\frac{3}{2}$x2-$\frac{9}{2}$x
=-$\frac{3}{2}$(x+$\frac{3}{2}$)2+$\frac{27}{8}$,
当x=-$\frac{3}{2}$时,S△BPC最大=$\frac{27}{8}$,
当x=-$\frac{3}{2}$时,y=-x2-2x+3=$\frac{15}{4}$,
∴点P坐标为:(-$\frac{3}{2}$,$\frac{15}{4}$);
(3)如图2,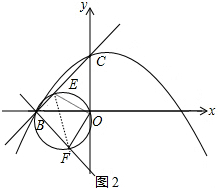 ∵OB=OC=3,
∵OB=OC=3,
∴△OBC为等腰直角三角形,
∴∠OBC=∠OCB=45°,
∵BF⊥BE,
∴∠FBO=45°,
∴∠OEF=∠OBF=45°,∠OFE=∠OBE=45°,
∴△OEF为等腰直角三角形,
∴OE=OF,∠EOF=90°,
∴S△OEF=OE•OF=OE2,
∴当OE最小时,△OEF面积取得最小值,
∵点E在线段BC上,
∴当OE⊥BC时,OE最小,此时点E是BC中点,
∴E(-$\frac{3}{2}$,$\frac{3}{2}$).
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和圆周角定理和等腰直角三角形的性质;会应用二次函数的性质解决最值问题;会利用待定系数法求函数解析式.利用圆周角定理得出EO=FO,进而分析得出OE最小时,△OEF面积取得最小值是解题关键.

 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案| A. | -2<a<2 | B. | a<0 | C. | -2<a<0 | D. | a<2 |
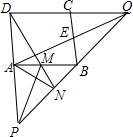 如图,在正方形ABcD中,M为AB中点,连结DM并延长DM到N,使NA2=NM•ND.
如图,在正方形ABcD中,M为AB中点,连结DM并延长DM到N,使NA2=NM•ND.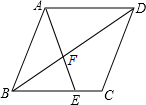 如图所示,在菱形ABCD中,E是BC上一点,且AE=AB,∠EAD=2∠BAE.求证:BE=AF.
如图所示,在菱形ABCD中,E是BC上一点,且AE=AB,∠EAD=2∠BAE.求证:BE=AF. 如图,已知△ABC内接于⊙O,点I是△ABC的内心,AI的延长线交BC于点E,交⊙O于点D.
如图,已知△ABC内接于⊙O,点I是△ABC的内心,AI的延长线交BC于点E,交⊙O于点D.