题目内容
1.代数式求值时我们常常会用到整体思想,简单的讲就是把一个代数式看作一个整体,进行适当的变形后代入求值.例如:已知a+2b=2,求1-a-2b的值,我们可以把a+2b看成一个整体,则-(a+2b)=-a-2b=-2,所以1-a-2b=1-2=-1.请你仿照上面的例子解决下面的问题:若a2-2a-2=0,则5+a-$\frac{1}{2}$a2=4.分析 先求得a2-2a=2,然后依据等式的性质得到a-$\frac{1}{2}$a2=-1,最后代入计算即可.
解答 解:∵a2-2a-2=0,
∴a2-2a=2.
等式两边同时乘以-$\frac{1}{2}$得:a-$\frac{1}{2}$a2=-1.
∴原式=5+(-1)=4.
故答案为:4.
点评 本题主要考查的是求代数式的值,整体代入是解题的关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
11.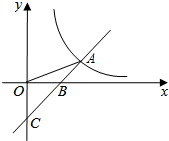 如图,直线y=x-b与y轴交于点C,与x轴交于点B,与反比例函数y=$\frac{m}{x}$的图象在第一象限交于点A(3,1),连接OA,则△AOB的面积为( )
如图,直线y=x-b与y轴交于点C,与x轴交于点B,与反比例函数y=$\frac{m}{x}$的图象在第一象限交于点A(3,1),连接OA,则△AOB的面积为( )
 如图,直线y=x-b与y轴交于点C,与x轴交于点B,与反比例函数y=$\frac{m}{x}$的图象在第一象限交于点A(3,1),连接OA,则△AOB的面积为( )
如图,直线y=x-b与y轴交于点C,与x轴交于点B,与反比例函数y=$\frac{m}{x}$的图象在第一象限交于点A(3,1),连接OA,则△AOB的面积为( )| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
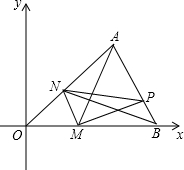 如图,在平面直角坐标中,△AOB的三个顶点的坐标分别是A(4,4),O(0,0),B(6,0),点M是射线OB上的一动点,过点M作MN∥AB,MN与射线OA交于点N,P是AB边上的任意点,连接AM,PM,PN,BN,设△PMN的面积为S.
如图,在平面直角坐标中,△AOB的三个顶点的坐标分别是A(4,4),O(0,0),B(6,0),点M是射线OB上的一动点,过点M作MN∥AB,MN与射线OA交于点N,P是AB边上的任意点,连接AM,PM,PN,BN,设△PMN的面积为S.