题目内容
10.(1)计算:(-2016)0+|1-$\sqrt{2}$|-2cos45°+${({-\frac{1}{3}})^{-2}}$(2)解不等式组:$\left\{\begin{array}{l}{x-3(x-2)≥4}\\{\frac{1+4x}{3}>x-1}\end{array}\right.$.
分析 (1)原式利用零指数幂、负整数指数幂,绝对值的代数意义,以及特殊角的三角函数值计算即可得到结果;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分即可确定出解集.
解答 解:(1)原式=1+$\sqrt{2}$-1-$\sqrt{2}$+9=9;
(2)$\left\{\begin{array}{l}{x-3(x-2)≥4①}\\{\frac{1+4x}{3}>x-1②}\end{array}\right.$,
由①得x≤1,
由②得:x>-4,
则不等式组的解集为-4<x≤1.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
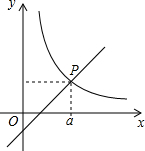 如图,直线y1=x-1与双曲线y2=$\frac{k}{x}$(x>0)交于点P(a,2),则关于x的不等式$\frac{k}{x}$>x-1≥0的解集为1≤x<3.
如图,直线y1=x-1与双曲线y2=$\frac{k}{x}$(x>0)交于点P(a,2),则关于x的不等式$\frac{k}{x}$>x-1≥0的解集为1≤x<3.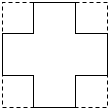 如图,将一块正方形铁片的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,已知盒子的容积为300cm3.若设原铁片的边长为xcm,则根据题意可得关于x的方程(x-3×2)(x-3×2)×3=300.
如图,将一块正方形铁片的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,已知盒子的容积为300cm3.若设原铁片的边长为xcm,则根据题意可得关于x的方程(x-3×2)(x-3×2)×3=300.
 已知多项式A=(x+2)2+x(1-x)-9
已知多项式A=(x+2)2+x(1-x)-9