题目内容
13.在平面直角坐标系中,线段AB的两个端点坐标分别为A(-1,1),B(2,3),将线段AB经过平移后得到线段A′B′,若点A的对应点A′(-1,-2),则点B的对应点B′的坐标是(2,0).分析 根据A点的坐标及对应点的坐标可得线段AB向下平移了3个单位,然后可得B′点的坐标.
解答 解:∵A(-1,1)平移后得到点A′的坐标为(-1,-2),
∴向下平移了3个单位,
∴B(2,3)的对应点坐标为(2,3-3),
即(2,0).
故答案为:(2,0).
点评 坐标与图形的变化--平移,关键是掌握点的坐标的变化规律.横坐标,右移加,左移减;纵坐标,上移加,下移减.

练习册系列答案
 能力评价系列答案
能力评价系列答案
相关题目
3.下列各分式中最简分式是( )
| A. | $\frac{{a}^{2}-{b}^{2}}{(a+b)^{2}}$ | B. | $\frac{{b}^{2}-{a}^{2}}{a+b}$ | C. | $\frac{a+b}{a-b}$ | D. | $\frac{20(a-b)}{15(a+b)}$ |
3.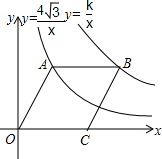 如图,点A在双曲线y=$\frac{4\sqrt{3}}{x}$(x>0)上,点B在双曲线y=$\frac{k}{x}$(x>0)上(点B在点A的右侧),且AB∥x轴,若四边形OABC是菱形,且∠AOC=60°,则k等于( )
如图,点A在双曲线y=$\frac{4\sqrt{3}}{x}$(x>0)上,点B在双曲线y=$\frac{k}{x}$(x>0)上(点B在点A的右侧),且AB∥x轴,若四边形OABC是菱形,且∠AOC=60°,则k等于( )
 如图,点A在双曲线y=$\frac{4\sqrt{3}}{x}$(x>0)上,点B在双曲线y=$\frac{k}{x}$(x>0)上(点B在点A的右侧),且AB∥x轴,若四边形OABC是菱形,且∠AOC=60°,则k等于( )
如图,点A在双曲线y=$\frac{4\sqrt{3}}{x}$(x>0)上,点B在双曲线y=$\frac{k}{x}$(x>0)上(点B在点A的右侧),且AB∥x轴,若四边形OABC是菱形,且∠AOC=60°,则k等于( )| A. | 6$\sqrt{3}$ | B. | 8$\sqrt{3}$ | C. | 9$\sqrt{3}$ | D. | 12$\sqrt{3}$ |
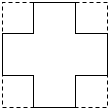 如图,将一块正方形铁片的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,已知盒子的容积为300cm3.若设原铁片的边长为xcm,则根据题意可得关于x的方程(x-3×2)(x-3×2)×3=300.
如图,将一块正方形铁片的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,已知盒子的容积为300cm3.若设原铁片的边长为xcm,则根据题意可得关于x的方程(x-3×2)(x-3×2)×3=300.