题目内容
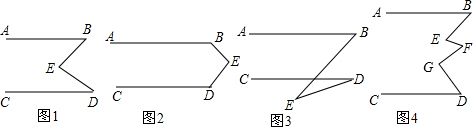
9.探究题:(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?
(2)若将点E移至图2的位置,此时∠B,∠D,∠E之间有什么关系?
(3)若将点E移至图3的位置,此时∠B,∠D,∠E之间的关系又如何?
(4)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?
分析 (1)过点E作EF∥AB,由平行线的性质可知∠B=∠BEF,∠D=∠DEF,再由角之间的关系即可得出结论;
(2)过点E作EF∥AB,由平行线的性质可知∠B+∠BEF=180°,∠D+∠DEF=180°,再由角之间的关系即可得出结论;
(3)过点E作EF∥AB,由平行线的性质可知∠B=∠BEF,∠D=∠DEF,再由角之间的关系即可得出结论;
(4)过点F作FM∥AB,用(1)的结论可知∠E=∠B+∠EFM,∠G=∠GFM+∠D,再由角之间的关系即可得出结论.
解答 解:(1)相等,过点E作EF∥AB,如图1所示.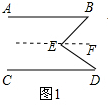
∵EF∥AB,
∴∠B=∠BEF,
∵EF∥AB∥CD,
∴∠D=∠DEF,
∴∠BED=∠BEF+∠DEF=∠B+∠D.
(2)过点E作EF∥AB,如图2所示.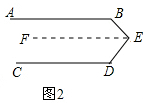
∵AB∥EF,
∴∠B+∠BEF=180°,
∵EF∥AB∥CD,
∴∠D+∠DEF=180°,
∴∠B+∠BEF+∠D+∠DEF=180°+180°,
∵∠E=∠BEF+∠DEF,
∴∠B+∠D+∠E=360°.
(3)过点E作EF∥AB,如图3所示.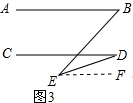
∵AB∥EF,
∴∠B=∠BEF,
∵EF∥AB∥CD,
∴∠D=∠DEF,
∴∠E=∠BEF-∠DEF=∠B-∠D.
(4)过点F作FM∥AB,如图4所示.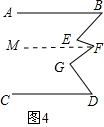
∵AB∥FM,结合(1)结论,
∴∠E=∠B+∠EFM,
∵FM∥AB∥CD,结合(1)结论,
∴∠G=∠GFM+∠D,
又∵∠F=∠EFM+∠GFM,
∴∠E+∠G=∠B+∠D+∠F.
点评 本题考查了平行线的性质以及角的计算,解题的关键是根据平行线的性质得出相等或互补的量.本题属于基础题,难度不大,在计算该题型题目时,根据平行线的性质找出相等(或互补)的角,再根据角与角之间的关系即可得出结论.

练习册系列答案
相关题目
19.已知x=1是一元一次方程2x-a=3的解,则a的值是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
14.小红家的收入分农业收入和其他收入两部分,今年农业收入是其他收入的1.5倍,预计明年农业收入将减少20%,而其他收入将增加25%,那么预计小红家明年的全年总收入( )
| A. | 减少2% | B. | 增加2% | C. | 减少0.2% | D. | 增加0.2% |
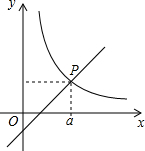 如图,直线y1=x-1与双曲线y2=$\frac{k}{x}$(x>0)交于点P(a,2),则关于x的不等式$\frac{k}{x}$>x-1≥0的解集为1≤x<3.
如图,直线y1=x-1与双曲线y2=$\frac{k}{x}$(x>0)交于点P(a,2),则关于x的不等式$\frac{k}{x}$>x-1≥0的解集为1≤x<3.
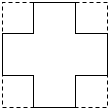 如图,将一块正方形铁片的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,已知盒子的容积为300cm3.若设原铁片的边长为xcm,则根据题意可得关于x的方程(x-3×2)(x-3×2)×3=300.
如图,将一块正方形铁片的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,已知盒子的容积为300cm3.若设原铁片的边长为xcm,则根据题意可得关于x的方程(x-3×2)(x-3×2)×3=300. 已知多项式A=(x+2)2+x(1-x)-9
已知多项式A=(x+2)2+x(1-x)-9