题目内容
11.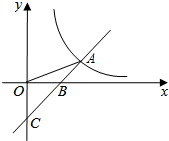 如图,直线y=x-b与y轴交于点C,与x轴交于点B,与反比例函数y=$\frac{m}{x}$的图象在第一象限交于点A(3,1),连接OA,则△AOB的面积为( )
如图,直线y=x-b与y轴交于点C,与x轴交于点B,与反比例函数y=$\frac{m}{x}$的图象在第一象限交于点A(3,1),连接OA,则△AOB的面积为( )| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
分析 由点A(3,1)在直线AB上,可得出关于b的一元一次方程,解方程即可得出直线AB的解析式,令y=0即可得出B点的坐标,套用三角形的面积公式即可得出结论.
解答 解:∵直线y=x-b过点A(3,1),
∴有1=3-b,解得b=2,
∴直线的AB的解析式为y=x-2.
令y=0,则有x-2=0,
解得x=2,即点B的坐标为(2,0).
△AOB的面积S=$\frac{1}{2}$×2×1=1.
故选A.
点评 本题考查了反比例函数与一次函数的交点问题、待定系数法求函数解析式以及三角形的面积公式,解题的关键是求出点B的坐标.本题属于基础题,难度不大,在解决该题中,要注意到那些信息有用,那些信息无用,此题中反比例的函数解析式用不到,只要找出点B的坐标套用三角形的面积公式即可得出结论.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
3.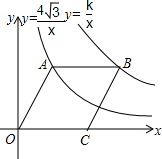 如图,点A在双曲线y=$\frac{4\sqrt{3}}{x}$(x>0)上,点B在双曲线y=$\frac{k}{x}$(x>0)上(点B在点A的右侧),且AB∥x轴,若四边形OABC是菱形,且∠AOC=60°,则k等于( )
如图,点A在双曲线y=$\frac{4\sqrt{3}}{x}$(x>0)上,点B在双曲线y=$\frac{k}{x}$(x>0)上(点B在点A的右侧),且AB∥x轴,若四边形OABC是菱形,且∠AOC=60°,则k等于( )
 如图,点A在双曲线y=$\frac{4\sqrt{3}}{x}$(x>0)上,点B在双曲线y=$\frac{k}{x}$(x>0)上(点B在点A的右侧),且AB∥x轴,若四边形OABC是菱形,且∠AOC=60°,则k等于( )
如图,点A在双曲线y=$\frac{4\sqrt{3}}{x}$(x>0)上,点B在双曲线y=$\frac{k}{x}$(x>0)上(点B在点A的右侧),且AB∥x轴,若四边形OABC是菱形,且∠AOC=60°,则k等于( )| A. | 6$\sqrt{3}$ | B. | 8$\sqrt{3}$ | C. | 9$\sqrt{3}$ | D. | 12$\sqrt{3}$ |
 已知多项式A=(x+2)2+x(1-x)-9
已知多项式A=(x+2)2+x(1-x)-9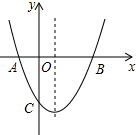 如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点,点P是抛物线上的一个动点,连接PA、PB,当S△PAB=8时,点P的坐标为(1+2$\sqrt{2}$,4)或(1-2$\sqrt{2}$,4)或(1,-4).
如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点,点P是抛物线上的一个动点,连接PA、PB,当S△PAB=8时,点P的坐标为(1+2$\sqrt{2}$,4)或(1-2$\sqrt{2}$,4)或(1,-4).