题目内容
已知圆内接正三角形的边心距为2cm,求它的边长.
考点:正多边形和圆
专题:
分析:如图,作辅助线;求出∠AOC=60°,借助直角三角形的边角关系求出AC的长,即可解决问题.
解答: 解:如图,连接OA、OB;
解:如图,连接OA、OB;
∵AB为⊙O的内接正三角形的一边,OC⊥AB于点C;
∴∠AOB=
=120°;
∵OA=OB,
∴∠AOC=
∠AOB=60°,AC=BC;
∵tan60°=
,而OC=2,
∴AC=2
,AB=4
(cm).
 解:如图,连接OA、OB;
解:如图,连接OA、OB;∵AB为⊙O的内接正三角形的一边,OC⊥AB于点C;
∴∠AOB=
| 360° |
| 3 |
∵OA=OB,
∴∠AOC=
| 1 |
| 2 |
∵tan60°=
| AC |
| OC |
∴AC=2
| 3 |
| 3 |
点评:该题主要考查了正多边形和圆的性质及其应用问题;解题的关键是作辅助线,灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
相关题目
 如图,壁虎在一个圆柱形油罐的下底边沿A处,它发现在B处有一只苍蝇,壁虎决定尽快捉到这只苍蝇,获得一顿美餐,请问壁虎从A处到B处的最短路线是什么?
如图,壁虎在一个圆柱形油罐的下底边沿A处,它发现在B处有一只苍蝇,壁虎决定尽快捉到这只苍蝇,获得一顿美餐,请问壁虎从A处到B处的最短路线是什么?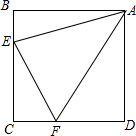 如图,四边形ABCD是边长为1的正方形,△ECF周长为2,求∠EAF的大小.
如图,四边形ABCD是边长为1的正方形,△ECF周长为2,求∠EAF的大小. 如图,在梯形ABCD中,已知AE平分∠BAD,AB=AD+BC,E是CD的中点.求证:BE平分∠ABC.
如图,在梯形ABCD中,已知AE平分∠BAD,AB=AD+BC,E是CD的中点.求证:BE平分∠ABC. 如图,在四边形ABCD中,AB=DC,∠ABC=∠DCB,点E、F分别在AB、BC上,且BE=2AE,CF=2DF.求证:∠BEC=∠CFB.
如图,在四边形ABCD中,AB=DC,∠ABC=∠DCB,点E、F分别在AB、BC上,且BE=2AE,CF=2DF.求证:∠BEC=∠CFB. 如图,在△ABC内的点P分别作三边的平行线.形成三个小三角形①②③,已知这三个三角形的面积分别是4,9,16,求△ABC的面积.
如图,在△ABC内的点P分别作三边的平行线.形成三个小三角形①②③,已知这三个三角形的面积分别是4,9,16,求△ABC的面积. 如图是某学校田径体育场一部分的示意图,跑道的长度是以该跑道的中心线来计算的,如以图中第一道的虚线部分来计算,第一条跑道每圈为400米,跑道分直道和弯道,直道为长相等的平行线段,弯道为同心的半圆型,弯道与直道相连接,已知直道BC的长86.96米,跑道的宽为l米.(π=3.14,结果精确到0.01)
如图是某学校田径体育场一部分的示意图,跑道的长度是以该跑道的中心线来计算的,如以图中第一道的虚线部分来计算,第一条跑道每圈为400米,跑道分直道和弯道,直道为长相等的平行线段,弯道为同心的半圆型,弯道与直道相连接,已知直道BC的长86.96米,跑道的宽为l米.(π=3.14,结果精确到0.01)