题目内容
如图，在△ABC内的点P分别作三边的平行线．形成三个小三角形①②③，已知这三个三角形的面积分别是4，9，16，求△ABC的面积．考点：相似三角形的判定与性质
专题：
分析：由条件可知△PKQ∽△HGP∽△DPE，再利用面积可求得相似比，可分别求出三个平行四边形的面积，可求得△ABC的面积．
解答：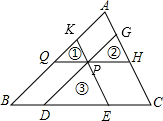
解：∵DG∥AB，QH∥BC，
∴△PKQ∽△DPE，
∴
=（
）2=
，
∴
=
，
∴
=
，
又∵△KQP∽△KBE，
∴
=（
）2=（
）2=
，
∴
=
，
∴S△KBE=36，
∴S四边形BDPQ=S△KBE-S△KQP-S△PDE=36-4-16=16，
同理可求得S四边形CEPH=24，S四边形AKPG=12，
∴S△ABC=16+12+24+16+9+4=81．
解：∵DG∥AB，QH∥BC，∴△PKQ∽△DPE，
∴
| S△KQP |
| S△PDE |
| KP |
| PE |
| 4 |
| 16 |
∴
| KP |
| PE |
| 1 |
| 2 |
∴
| KP |
| KE |
| 1 |
| 3 |
又∵△KQP∽△KBE，
∴
| S△KQP |
| S△KBE |
| KP |
| KE |
| 1 |
| 3 |
| 1 |
| 9 |
∴
| 4 |
| S△KBE |
| 1 |
| 9 |
∴S△KBE=36，
∴S四边形BDPQ=S△KBE-S△KQP-S△PDE=36-4-16=16，
同理可求得S四边形CEPH=24，S四边形AKPG=12，
∴S△ABC=16+12+24+16+9+4=81．
点评：本题主要考查相似三角形的判定和性质，掌握相似三角形的面积比等于相似比是解题的关键，注意方程思想和比例性质的应用．
练习册系列答案
相关题目
如图，在七边形ABCDEFG中，∠D=90°，其他六个角彼此相等，且AB=2，EF=FG=2| 2 |
A、26+16
| ||
B、30+15
| ||
C、32+16
| ||
D、15+30
|
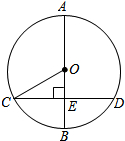如图，AB是⊙O的直径，弦CD⊥AB于点E，连结OC，若OE=| 3 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，D是Rt△ABC的直角边BC上的点，以BD为直径的⊙O交斜边AB于E，EC交⊙O于点F，BF的延长线交AC于点G，求证：FG•AC=FC•AE．
如图，D为等腰直角△ABC的斜边AB上一点，点E在BC上，且DC=DE，求
