题目内容
 如图,在四边形ABCD中,AB=DC,∠ABC=∠DCB,点E、F分别在AB、BC上,且BE=2AE,CF=2DF.求证:∠BEC=∠CFB.
如图,在四边形ABCD中,AB=DC,∠ABC=∠DCB,点E、F分别在AB、BC上,且BE=2AE,CF=2DF.求证:∠BEC=∠CFB.考点:全等三角形的判定与性质
专题:证明题
分析:根据题意可得∠ABC=∠DCB,易证BE=CF,即可证明△EBC≌△FCB,即可解题.
解答:解:∵BE=2AE,CF=2DF,AB=DC,
∴BE=CF,
在△EBC和△FCB中,
,
∴△EBC≌△FCB(SAS),
∴∠BEC=∠CFB.
∴BE=CF,
在△EBC和△FCB中,
|
∴△EBC≌△FCB(SAS),
∴∠BEC=∠CFB.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中求证△EBC≌△FCB是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
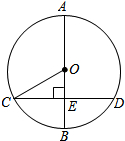 如图,AB是⊙O的直径,弦CD⊥AB于点E,连结OC,若OE=
如图,AB是⊙O的直径,弦CD⊥AB于点E,连结OC,若OE=| 3 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在Rt△ABC中,AC=BC,AC⊥BC,AE⊥BE,AE=
如图,在Rt△ABC中,AC=BC,AC⊥BC,AE⊥BE,AE=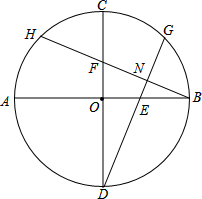 在⊙O中,已知直径AB与直径CD垂直于O,E在OB上,F在OC,且OE=OF,连接DE且延长交⊙O于G,连接BF且延长交⊙O于H,BH与DG相交于N.求证:BH⊥GD.
在⊙O中,已知直径AB与直径CD垂直于O,E在OB上,F在OC,且OE=OF,连接DE且延长交⊙O于G,连接BF且延长交⊙O于H,BH与DG相交于N.求证:BH⊥GD. 如图,D是Rt△ABC的直角边BC上的点,以BD为直径的⊙O交斜边AB于E,EC交⊙O于点F,BF的延长线交AC于点G,求证:FG•AC=FC•AE.
如图,D是Rt△ABC的直角边BC上的点,以BD为直径的⊙O交斜边AB于E,EC交⊙O于点F,BF的延长线交AC于点G,求证:FG•AC=FC•AE. 如图,在△ABC中,点D、E、F分别是边BC、CA、AB的中点,△DEF与△ABC是否位似?如果位似,找出位似中心?
如图,在△ABC中,点D、E、F分别是边BC、CA、AB的中点,△DEF与△ABC是否位似?如果位似,找出位似中心?