题目内容
12.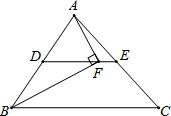 如图,DE为△ABC的中位线,点F在DE上,且∠AFB为直角,若AB=8,BC=10,则EF的长为1.
如图,DE为△ABC的中位线,点F在DE上,且∠AFB为直角,若AB=8,BC=10,则EF的长为1.
分析 根据三角形的中位线定理求得DE的长,然后根据FD是直角△ABF斜边上的中线,求得FD的长,则EF即可求得.
解答 解:∵DE为△ABC的中位线,
∴DE=$\frac{1}{2}$BC=$\frac{1}{2}$×10=5,
∵∠AFB为直角,D是AB的中点,即FD是直角△ABF的中线,
∴FD=$\frac{1}{2}$AB=$\frac{1}{2}$×8=4.
∴EF=DE-FD=5-4=1.
故答案是:1.
点评 本题考查了三角形的中位线定理以及直角三角形的性质,直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
7.已知在四边形ABCD中,AB∥CD,添加下列一个条件后,一定能判定四边形ABCD是平行四边形的是( )
| A. | AD=BC | B. | AC=BD | C. | ∠A=∠C | D. | ∠A=∠B |
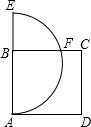 如图,正方形ABCD的边长等于3,点E是AB延长线上一点,且AE=5,以AE为直径的半圆交BC于点F,则BF=$\sqrt{6}$.
如图,正方形ABCD的边长等于3,点E是AB延长线上一点,且AE=5,以AE为直径的半圆交BC于点F,则BF=$\sqrt{6}$.
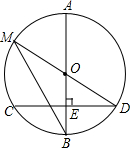 如图,AB是⊙O的直径,弦CD⊥AB于点E,且CD=24,点M在⊙O上,MD经过圆心O,联结MB.
如图,AB是⊙O的直径,弦CD⊥AB于点E,且CD=24,点M在⊙O上,MD经过圆心O,联结MB. 在平面直角坐标系中,一个二次函数的图象经过A(1,0)、B(3,0)两点.
在平面直角坐标系中,一个二次函数的图象经过A(1,0)、B(3,0)两点.