题目内容
1. 在平面直角坐标系中,一个二次函数的图象经过A(1,0)、B(3,0)两点.
在平面直角坐标系中,一个二次函数的图象经过A(1,0)、B(3,0)两点.(1)写出这个二次函数图象的对称轴;
(2)设这个二次函数图象的顶点为D,与y轴交于点C,它的对称轴与x轴交于点E,连接AC、DE和DB.当△AOC与△DEB相似时,求这个函数的表达式.
分析 (1)根据二次函数对称性得出对称轴即可;
(2)首先求出C,D点坐标,进而得出CO的长,利用当△AOC与△DEB相似时,根据①假设∠OCA=∠EBD,②假设∠OCA=∠EDB,分别求出即可.
解答 解:(1)∵二次函数的图象经过点A(1,0)、B(3,0)两点,
∴二次函数图象的对称轴为直线x=2;
(2)如图,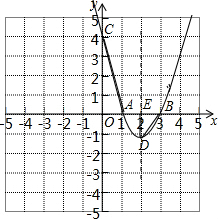
设二次函数的表达式为:y=a(x-1)(x-3)(a≠0),
当x=0时,y=3a,当x=2时,y=-a,
∴点C坐标为:(0,3a),顶点D坐标为:(2,-a),
∴OC=|3a|,
又∵A(1,0),E(2,0),
∴AO=1,EB=1,DE=|-a|=|a|,
当△AOC与△DEB相似时,
①假设∠OCA=∠EBD,
可得$\frac{AO}{DE}=\frac{OC}{EB}$,
即$\frac{1}{|a|}=\frac{|3a|}{1}$,
∴a=$\frac{\sqrt{3}}{3}$ 或a=-$\frac{\sqrt{3}}{3}$,
②假设∠OCA=∠EDB,可得$\frac{AO}{BE}=\frac{OC}{ED}$,
∴$\frac{1}{1}=\frac{|3a|}{|a|}$,此方程无解,
综上所述,所得二次函数的表达式为:
y=$\frac{\sqrt{3}}{3}{x}^{2}-\frac{4\sqrt{3}}{3}x+\sqrt{3}$ 或y=$-\frac{\sqrt{3}}{3}{x}^{2}+\frac{4\sqrt{3}}{3}x-\sqrt{3}$.
点评 此题主要考查了二次函数的综合应用以及相似三角形的判定与性质等知识,注意分类讨论思想的应用是解题关键.

练习册系列答案
相关题目
11.在下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. | 直角三角形 | B. | 正五边形 | C. | 菱形 | D. | 平行四边形 |
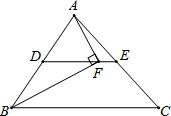 如图,DE为△ABC的中位线,点F在DE上,且∠AFB为直角,若AB=8,BC=10,则EF的长为1.
如图,DE为△ABC的中位线,点F在DE上,且∠AFB为直角,若AB=8,BC=10,则EF的长为1.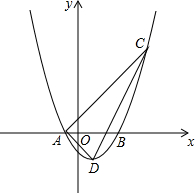 如图,在平面直角坐标系中,O为坐标原点,开口向上的抛物线与x轴交于点A(-1,0)和点B(3,0),D为抛物线的顶点,直线AC与抛物线交C(5,6).
如图,在平面直角坐标系中,O为坐标原点,开口向上的抛物线与x轴交于点A(-1,0)和点B(3,0),D为抛物线的顶点,直线AC与抛物线交C(5,6).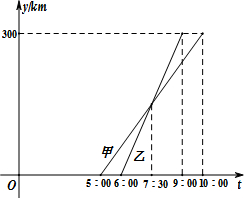 甲、乙两车从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,则当乙车到达B城时,甲车离B城的距离为60km.
甲、乙两车从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,则当乙车到达B城时,甲车离B城的距离为60km.
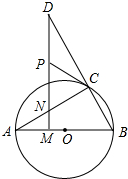 如图所示,△ABC的外接圆圆心O在AB上,点D是BC延长线上一点,DM⊥AB于M,交AC于N,且AC=CD.CP是△CDN的边ND上的中线.
如图所示,△ABC的外接圆圆心O在AB上,点D是BC延长线上一点,DM⊥AB于M,交AC于N,且AC=CD.CP是△CDN的边ND上的中线.