题目内容
2.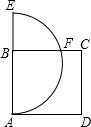 如图,正方形ABCD的边长等于3,点E是AB延长线上一点,且AE=5,以AE为直径的半圆交BC于点F,则BF=$\sqrt{6}$.
如图,正方形ABCD的边长等于3,点E是AB延长线上一点,且AE=5,以AE为直径的半圆交BC于点F,则BF=$\sqrt{6}$.
分析 作出AE的中点O,连接OF,在直角△OBF中利用勾股定理即可求得BF的长.
解答  解:作出AE的中点O,连接OF.
解:作出AE的中点O,连接OF.
则OF=OA=$\frac{1}{2}$AE=$\frac{5}{2}$,OB=AB-OA=3-$\frac{5}{2}$=$\frac{1}{2}$.
在直角△OBF中,BF=$\sqrt{O{F}^{2}-O{B}^{2}}$=$\sqrt{(\frac{5}{2})^{2}-(\frac{1}{2})^{2}}$=$\sqrt{6}$.
故答案是:$\sqrt{6}$.
点评 本题考查了勾股定理,正确作出辅助线,构造直角三角形是解决本题的关键.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
17.下列事件是确定事件的是( )
| A. | 阴天一定会下雨 | |
| B. | 黑暗中从5把不同的钥匙中随意摸出一把,用它打开了门 | |
| C. | 打开电视机,任选一个频道,屏幕上正在播放新闻联播 | |
| D. | 在五个抽屉中任意放入6本书,则至少有一个抽屉里有两本书 |
14.下列各数中,整数部分为3的数是( )
| A. | π | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
11.在下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. | 直角三角形 | B. | 正五边形 | C. | 菱形 | D. | 平行四边形 |
 已知y是x的反比例函数,且当x=2时,y=-3,
已知y是x的反比例函数,且当x=2时,y=-3,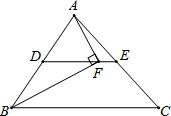 如图,DE为△ABC的中位线,点F在DE上,且∠AFB为直角,若AB=8,BC=10,则EF的长为1.
如图,DE为△ABC的中位线,点F在DE上,且∠AFB为直角,若AB=8,BC=10,则EF的长为1.