题目内容
18.阅读理解:符号:“$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$”称为二阶行列式,规定它的运算法则如下:$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc.例如:$|\begin{array}{l}{5}&{6}\\{7}&{8}\end{array}|$的计算方法为:$|\begin{array}{l}{5}&{6}\\{7}&{8}\end{array}|$=5×8-6×7=-2,请根据阅读理解,化简二阶行列式:$|\begin{array}{l}{a+1}&{a}\\{\frac{1}{1-a}}&{1}\end{array}|$.
分析 原式利用题中的新定义化简,计算即可得到结果.
解答 解:根据题中的新定义得:$|\begin{array}{l}{a+1}&{a}\\{\frac{1}{1-a}}&{1}\end{array}|$=a+1-$\frac{a}{1-a}$=$\frac{(a+1)(a-1)}{a-1}$+$\frac{a}{a-1}$=$\frac{{a}^{2}+a-1}{a-1}$.
点评 此题考查了分式的混合运算,弄清题中的新定义是解本题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
13.某市统计局发布的统计公报显示,2006年到2010年,某市GDP增长率分别为9.9%、10.1%、10.3%、10.5%、10.2%.经济评论员说,这5年该的GDP增长率相当平稳,从统计学的角度看,“增长率相当平稳”说明这组数据( )比较小.
| A. | 中位数 | B. | 方差 | C. | 众数 | D. | 平均数 |
10.圆的半径为4,圆心到直线l的距离为3,则直线l与⊙O位置关系是( )
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 相切或相交 |
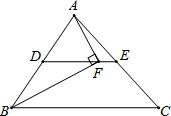 如图,DE为△ABC的中位线,点F在DE上,且∠AFB为直角,若AB=8,BC=10,则EF的长为1.
如图,DE为△ABC的中位线,点F在DE上,且∠AFB为直角,若AB=8,BC=10,则EF的长为1.
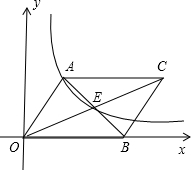 如图,平行四边形AOBC中,对角线交于点E,双曲线y=$\frac{k}{x}$(k>0)经过A、E两点,若平行四边形AOBC的面积为12,则k=4.
如图,平行四边形AOBC中,对角线交于点E,双曲线y=$\frac{k}{x}$(k>0)经过A、E两点,若平行四边形AOBC的面积为12,则k=4.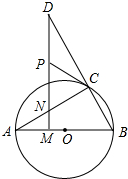 如图所示,△ABC的外接圆圆心O在AB上,点D是BC延长线上一点,DM⊥AB于M,交AC于N,且AC=CD.CP是△CDN的边ND上的中线.
如图所示,△ABC的外接圆圆心O在AB上,点D是BC延长线上一点,DM⊥AB于M,交AC于N,且AC=CD.CP是△CDN的边ND上的中线.