题目内容
17.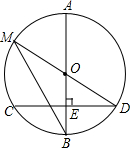 如图,AB是⊙O的直径,弦CD⊥AB于点E,且CD=24,点M在⊙O上,MD经过圆心O,联结MB.
如图,AB是⊙O的直径,弦CD⊥AB于点E,且CD=24,点M在⊙O上,MD经过圆心O,联结MB.(1)若BE=8,求⊙O的半径;
(2)若∠DMB=∠D,求线段OE的长.
分析 (1)根据垂径定理求出DE的长,设出半径,根据勾股定理,列出方程求出半径;
(2)根据OM=OB,证出∠M=∠B,根据∠M=∠D,求出∠D的度数,根据锐角三角函数求出OE的长.
解答 解:(1)设⊙O的半径为x,则OE=x-8,
∵CD=24,由垂径定理得,DE=12,
在Rt△ODE中,OD2=DE2+OE2,
x2=(x-8)2+122,
解得:x=13.
(2)∵OM=OB,
∴∠M=∠B,
∴∠DOE=2∠M,
又∠M=∠D,
∴∠D=30°,
在Rt△OED中,∵DE=12,∠D=30°,
∴OE=4$\sqrt{3}$.
点评 本题考查的是垂径定理、勾股定理和圆周角定理的综合运用,灵活运用定理求出线段的长度、列出方程是解题的关键,本题综合性较强,锻炼学生的思维能力.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
5.如果关于x的一元二次方程x2-4x+k=0有两个不相等的实数根,那么k的取值范围是( )
| A. | k<4 | B. | k>4 | C. | k<0 | D. | k>0 |
2.下列命题中,假命题是( )
| A. | 没有公共点的两圆叫两圆相离 | |
| B. | 相交两圆的交点关于这两个圆的连心线所在直线对称 | |
| C. | 联结相切两圆圆心的直线必经过切点 | |
| D. | 内含的两个圆的圆心距大于零 |
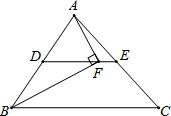 如图,DE为△ABC的中位线,点F在DE上,且∠AFB为直角,若AB=8,BC=10,则EF的长为1.
如图,DE为△ABC的中位线,点F在DE上,且∠AFB为直角,若AB=8,BC=10,则EF的长为1.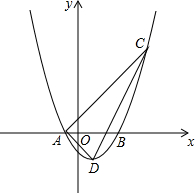 如图,在平面直角坐标系中,O为坐标原点,开口向上的抛物线与x轴交于点A(-1,0)和点B(3,0),D为抛物线的顶点,直线AC与抛物线交C(5,6).
如图,在平面直角坐标系中,O为坐标原点,开口向上的抛物线与x轴交于点A(-1,0)和点B(3,0),D为抛物线的顶点,直线AC与抛物线交C(5,6).