题目内容
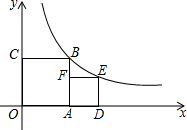
9. 已知点P是正方形ABCD边AD上的一个动点,AE⊥BP,CF⊥BP,垂足点分別为点E,F,AD=4.PM∥FC交DC于M点
已知点P是正方形ABCD边AD上的一个动点,AE⊥BP,CF⊥BP,垂足点分別为点E,F,AD=4.PM∥FC交DC于M点 (1)证明:△APB∽△DMP;
(2)当点P在边AD上运动时,设AP的长为x,问:当x取何值时,线段DM的长取最大值,并求出这个最大值.
分析 (1)由正方形的性质和已知条件得出已知∠DPM=∠ABP,即可得出△APB∽△DMP;
(2)设AP=x,则PD=4-x,由相似三角形的性质得出比例式,得出DM是关于x的二次函数,求出DM的最大值即可.
解答 (1)证明:∵四边形ABCD是正方形,
∴∠BAP=∠D=90°,
∴∠ABP+∠APB=90°,
∵CF⊥BP,PM∥CF,
∴PM⊥BP,
∴∠APB+∠DPM=90°,
∴∠ABP=∠DPM,
∴△APB∽△DMP;
(2)解:设AP=x,则PD=4-x,AB=AD=4,
∵△APB∽△DMP,
∴$\frac{DM}{AP}=\frac{PD}{BA}$,即$\frac{DM}{4-x}=\frac{x}{4}$,
∴DM=$\frac{x(4-x)}{4}$=x-$\frac{1}{4}$x2=-$\frac{1}{4}$(x-2)2+1,
∴当x=2时,即点P是AD的中点时,DM有最大值,最大值为1.
点评 本题主要考查正方形的性质、相似三角形的判定与性质;熟练掌握正方形的性质,证明三角形相似是解决问题的关键.

练习册系列答案
相关题目
2.延庆区由于生态质量良好、自然资源丰富,成为北京的生态涵养区,是其生态屏障和水源保护地.为降低空气污染,919公交公司决定全部更换节能环保的燃气公交车.计划购买A型和B型两种公交车共10辆,其中每台的价格,年载客量如表:
若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求a,b的值;
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次.请你设计一个方案,使得购车总费用最少.
| A型 | B型 | |
| 价格(万元/台) | a | b |
| 年载客量(万人/年) | 60 | 100 |
(1)求a,b的值;
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次.请你设计一个方案,使得购车总费用最少.
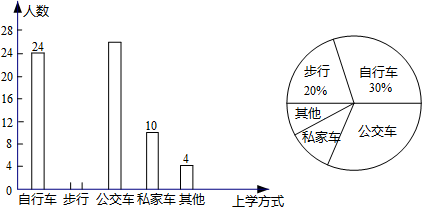
17.某体育用品商店为了解5月份的销售情况,对本月各类商品的销售情况进行调查,并将调查的结果绘制成如下两幅不完整的统计图

(1)请根据图中提供的信息,将条形图补充完整;
(2)该商店准备按5月份球类商品销量的数量购进球类商品,含篮球、足球、排球三种球,预计恰好用完进货款共3600元,设购进篮球x个,足球y个,三种球的进价和售价如表:
求出y与x之间的函数关系式;
(3)在(2)中的进价和售价的条件下,据实际情况,预计足球销售超过60个后,这种球就会产生滞销.
①假设所购进篮球、足球、排球能全部售出,求出预估利润P(元)与x(个)的函数关系式;
②求出预估利润的最大值,并写出此时购进三种球各多少个.

(1)请根据图中提供的信息,将条形图补充完整;
(2)该商店准备按5月份球类商品销量的数量购进球类商品,含篮球、足球、排球三种球,预计恰好用完进货款共3600元,设购进篮球x个,足球y个,三种球的进价和售价如表:
| 类别 | 篮球 | 足球 | 排球 |
| 进价(单位:元/个) | 50 | 30 | 20 |
| 预售价(单位:元/个) | 70 | 45 | 25 |
(3)在(2)中的进价和售价的条件下,据实际情况,预计足球销售超过60个后,这种球就会产生滞销.
①假设所购进篮球、足球、排球能全部售出,求出预估利润P(元)与x(个)的函数关系式;
②求出预估利润的最大值,并写出此时购进三种球各多少个.
18. 如若正方形OABC的顶点B和正方形ADEF的顶点E都在反比例函数y=$\frac{1}{x}$(x>0)的图象上,则E点的坐标是( )
如若正方形OABC的顶点B和正方形ADEF的顶点E都在反比例函数y=$\frac{1}{x}$(x>0)的图象上,则E点的坐标是( )
 如若正方形OABC的顶点B和正方形ADEF的顶点E都在反比例函数y=$\frac{1}{x}$(x>0)的图象上,则E点的坐标是( )
如若正方形OABC的顶点B和正方形ADEF的顶点E都在反比例函数y=$\frac{1}{x}$(x>0)的图象上,则E点的坐标是( )| A. | $({\frac{{\sqrt{5}-1}}{2},\frac{{\sqrt{5}+1}}{2}})$ | B. | $({\frac{{\sqrt{5}+1}}{2},\frac{{\sqrt{5}-1}}{2}})$ | C. | $({\frac{{\sqrt{5}}}{2},-\frac{{\sqrt{5}}}{2}})$ | D. | (1,1) |
 如图,已知在三角形ABC中,∠A=56°,AB=8cm,BC=12cm,现将″三角形ABC沿直线BC向左平移xcm,得到新的三角形DEF,DF交AB于点G.
如图,已知在三角形ABC中,∠A=56°,AB=8cm,BC=12cm,现将″三角形ABC沿直线BC向左平移xcm,得到新的三角形DEF,DF交AB于点G. 某学校期末考试要给学生印制复习资料若干份,印刷厂有甲、乙两种收费方式,除按印刷份数收取印刷费用外,甲种方式还收取制版费,而乙种不需要,两种印刷方式的费用y(元)与印刷份数x(份)之间的函数关系如图所示:
某学校期末考试要给学生印制复习资料若干份,印刷厂有甲、乙两种收费方式,除按印刷份数收取印刷费用外,甲种方式还收取制版费,而乙种不需要,两种印刷方式的费用y(元)与印刷份数x(份)之间的函数关系如图所示: