题目内容
20. 如图,已知在三角形ABC中,∠A=56°,AB=8cm,BC=12cm,现将″三角形ABC沿直线BC向左平移xcm,得到新的三角形DEF,DF交AB于点G.
如图,已知在三角形ABC中,∠A=56°,AB=8cm,BC=12cm,现将″三角形ABC沿直线BC向左平移xcm,得到新的三角形DEF,DF交AB于点G.(1)求∠BGF的度数;
(2)若x=3,BG=6cm,求图中阴影部分的面积.
分析 (1)直接利用平移的性质得出对应线段以及对应角的关系进而得出答案;
(2)直接利用平移的性质结合三角形面积求法得出答案.
解答 解:(1)∵∠A=56°,现将″三角形ABC沿直线BC向左平移xcm,得到新的三角形DEF,
∴∠D=56°,DE∥BG,
∴∠BGF=56°;
(2)∵x=3,BG=6cm,
∴AG=2cm,BF=9cm,
∴图中阴影部分的面积为:$\frac{1}{2}$×8×12-$\frac{1}{2}$×6×9=21(cm2).
点评 此题主要考查了平移的性质,正确应用平移的性质是解题关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
11. 如图,是雷达探测器测得的结果,图中显示在点A,B,C,D,E,F处有目标出现,目标的表示方法为(r,α),其中,r表示目标与探测器的距离;α表示以正东为始边,逆时针旋转后的角度.例如,点A,D的位置表示为A(5,30°),D(4,240°).用这种方法表示点B,C,E,F的位置,其中正确的是( )
如图,是雷达探测器测得的结果,图中显示在点A,B,C,D,E,F处有目标出现,目标的表示方法为(r,α),其中,r表示目标与探测器的距离;α表示以正东为始边,逆时针旋转后的角度.例如,点A,D的位置表示为A(5,30°),D(4,240°).用这种方法表示点B,C,E,F的位置,其中正确的是( )
 如图,是雷达探测器测得的结果,图中显示在点A,B,C,D,E,F处有目标出现,目标的表示方法为(r,α),其中,r表示目标与探测器的距离;α表示以正东为始边,逆时针旋转后的角度.例如,点A,D的位置表示为A(5,30°),D(4,240°).用这种方法表示点B,C,E,F的位置,其中正确的是( )
如图,是雷达探测器测得的结果,图中显示在点A,B,C,D,E,F处有目标出现,目标的表示方法为(r,α),其中,r表示目标与探测器的距离;α表示以正东为始边,逆时针旋转后的角度.例如,点A,D的位置表示为A(5,30°),D(4,240°).用这种方法表示点B,C,E,F的位置,其中正确的是( )| A. | B(2,90°) | B. | C(2,120°) | C. | E(3,120°) | D. | F(4,210°) |
12.二次函数y=ax2+bx+c图象上部分点的坐标满足表格:
则该函数图象的顶点坐标为( )
| x | … | -3 | -2 | -1 | 0 | 1 | … |
| y | … | -3 | -2 | -3 | -6 | -11 | … |
| A. | (-3,-3) | B. | (-2,-2) | C. | (-1,-3) | D. | (0,-6) |
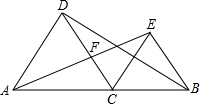 如图,点C是线段AB上一点,△ACD和△BCE都是等边三角形,连结AE,BD,设AE交CD于点F.
如图,点C是线段AB上一点,△ACD和△BCE都是等边三角形,连结AE,BD,设AE交CD于点F. A、B两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,甲车驶往B城,乙车驶往A城,甲车在高速公路上匀速行驶,距B城高速公路入口处的距离y(千米)与时间x(时)之间的关系如图.
A、B两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,甲车驶往B城,乙车驶往A城,甲车在高速公路上匀速行驶,距B城高速公路入口处的距离y(千米)与时间x(时)之间的关系如图. 已知点P是正方形ABCD边AD上的一个动点,AE⊥BP,CF⊥BP,垂足点分別为点E,F,AD=4.PM∥FC交DC于M点
已知点P是正方形ABCD边AD上的一个动点,AE⊥BP,CF⊥BP,垂足点分別为点E,F,AD=4.PM∥FC交DC于M点  如图,先将三角形ABC向左平移3个单位长度,再向下平移4个单位长度,得到三角形A1B1C1.
如图,先将三角形ABC向左平移3个单位长度,再向下平移4个单位长度,得到三角形A1B1C1.