Question

18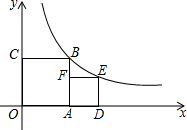．如若正方形OABC的顶点B和正方形ADEF的顶点E都在反比例函数y=$\frac{1}{x}$（x＞0）的图象上，则E点的坐标是（　　）

• A． $（{\frac{{\sqrt{5}-1}}{2}，\frac{{\sqrt{5}+1}}{2}}）$
• B． $（{\frac{{\sqrt{5}+1}}{2}，\frac{{\sqrt{5}-1}}{2}}）$
• C． $（{\frac{{\sqrt{5}}}{2}，-\frac{{\sqrt{5}}}{2}}）$
• D． （1，1）

Answer 1

分析 在正方形ABCO中四边都相等，由反比例函数比例系数k的几何意义可得，正方形OABC的面积为1，求得OA=1．若设AD=DE=m，则OD=1+m，再根据反比例函数图象上点的坐标特征，可列方程求得m的值，即可得出E点的坐标．

解答 解：依据反比例函数比例系数k的几何意义可得，正方形OABC的面积为1，
∴OA的长为1，
设AD=DE=m，则OD=1+m，
∴E（1+m，m），
将E（1+m，m）代入反比例函数y=$\frac{1}{x}$可得，
m（1+m）=1，
解得，m₁=$\frac{-1+\sqrt{5}}{2}$，m₂=$\frac{-1-\sqrt{5}}{2}$（不合题意，舍去），
∴1+m=$\frac{1+\sqrt{5}}{2}$，
故点E的坐标是（$\frac{1+\sqrt{5}}{2}$，$\frac{-1+\sqrt{5}}{2}$）．
故选（B）

点评 本题主要考查反比例函数图象上点的坐标特征，根据正方形的四条边都相等，并利用两正方形的边长表示出点B、E的坐标是解题的关键．在反比例函数y=$\frac{k}{x}$图象上任取一点，过这点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|，这是反比例函数比例系数k的几何意义．