题目内容
4. 某学校期末考试要给学生印制复习资料若干份,印刷厂有甲、乙两种收费方式,除按印刷份数收取印刷费用外,甲种方式还收取制版费,而乙种不需要,两种印刷方式的费用y(元)与印刷份数x(份)之间的函数关系如图所示:
某学校期末考试要给学生印制复习资料若干份,印刷厂有甲、乙两种收费方式,除按印刷份数收取印刷费用外,甲种方式还收取制版费,而乙种不需要,两种印刷方式的费用y(元)与印刷份数x(份)之间的函数关系如图所示:(1)填空:甲种收费方式的函数关系式是y1=0.1x+16(x≥0),乙种收费方式的函数关系式是y2=0.2x(x≥0).
(2)若需印刷100-400份(含100和400)份复习资料,选择哪种印刷方式比较合算.
分析 (1)设甲种收费的函数关系式y1=kx+b,乙种收费的函数关系式是y2=k1x,直接运用待定系数法就可以求出结论;
(2)由(1)的解析式分三种情况进行讨论,当y1>y2时,当y1=y2时,当y1<y2时分别求出x的取值范围就可以得出选择方式.
解答 解:(1)设甲种收费的函数关系式y1=kx+b,乙种收费的函数关系式是y2=k1x,由题意,得
$\left\{\begin{array}{l}{16=b}\\{26=100k+b}\end{array}\right.$,20=100k1,
解得:$\left\{\begin{array}{l}{k=0.1}\\{b=6}\end{array}\right.$,k1=0.2,
∴y1=0.1x+16(x≥0),y2=0.2x(x≥0);
故答案为:y1=0.1x+16(x≥0),y2=0.2x(x≥0);
(2)由0.1x+16>0.2x,得x<160,
由0.1x+16=0.2x,得x=160,
由0.1x+16<0.2x,得x>160,
由此可知:当100≤x<160时,选择乙种收费方式比较合算;
当x=160时,选择甲、乙两种收费方式都可以;
当160<x≤400时,选择甲种收费方式比较合算.
点评 本题考查待定系数法求一次函数的解析式的运用,运用函数的解析式解答方案设计的运用,解答时求出函数解析式是关键,分类讨论设计方案是难点.

练习册系列答案
相关题目
12.二次函数y=ax2+bx+c图象上部分点的坐标满足表格:
则该函数图象的顶点坐标为( )
| x | … | -3 | -2 | -1 | 0 | 1 | … |
| y | … | -3 | -2 | -3 | -6 | -11 | … |
| A. | (-3,-3) | B. | (-2,-2) | C. | (-1,-3) | D. | (0,-6) |
16. 如图,已知AB=2AD,AC=2AE,则下列结论错误的是( )
如图,已知AB=2AD,AC=2AE,则下列结论错误的是( )
 如图,已知AB=2AD,AC=2AE,则下列结论错误的是( )
如图,已知AB=2AD,AC=2AE,则下列结论错误的是( )| A. | △ABD∽△ACE | B. | ∠B=∠C | C. | BD=2CE | D. | AB•EC=AC•BD |
14.某同学画出了如图所示的几何体的三种视图,其中正确的是( )

| A. | ①② | B. | ①③ | C. | ②③ | D. | ② |
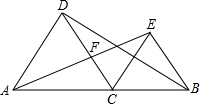 如图,点C是线段AB上一点,△ACD和△BCE都是等边三角形,连结AE,BD,设AE交CD于点F.
如图,点C是线段AB上一点,△ACD和△BCE都是等边三角形,连结AE,BD,设AE交CD于点F. 已知点P是正方形ABCD边AD上的一个动点,AE⊥BP,CF⊥BP,垂足点分別为点E,F,AD=4.PM∥FC交DC于M点
已知点P是正方形ABCD边AD上的一个动点,AE⊥BP,CF⊥BP,垂足点分別为点E,F,AD=4.PM∥FC交DC于M点