题目内容
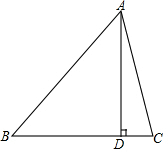如图，在△ABC中，AD⊥BC于点D，AB=2| 2 |
| 5 |
考点：勾股定理
专题：
分析：如图，设AD=x，则在直角△ABD和直角△ACD中，利用勾股定理分别求得BD、CD的长度，则易列出关于x的方程，通过解方程求得x的值即可．
解答：解：如图，设AD=x．依题意得
+
=BD+CD=BC．
即
+
=
，
解得 x=
即AD=
．
| AB2-AD2 |
| AC2-AD2 |
即
| 8-x2 |
| 5-x2 |
| 5 |
解得 x=
2
| ||
| 5 |
即AD=
2
| ||
| 5 |
点评：本题考查了勾股定理．此题也可以设CD=x，然后分别在直角△ABD和直角△ACD中，利用x来表示AD的长度，由此列出AB2-BD2=AC2-CD2，将相关线段的长度代入进行解答即可．
练习册系列答案
智趣暑假温故知新系列答案
相关题目
已知AD=AE，AF=AG，AD⊥BD，AE⊥CE，求证：AB=AC．
如图，用数字标注的角中，共有四对内错角，请把它们一一写出，并说明哪两条直线被哪一条直线所截得的内错角．
如图，已知：AB=CB，AD=CD，求证：∠A=∠C．
如图，已知?ABCD的周长为30cm，AE⊥BC于点E，AF⊥DC于点F，AE：AF=2：3，∠C=120°，求?ABCD的面积．
用小立方体搭几何体，主视图和俯视图如图所示，这样的几何正方体最少需要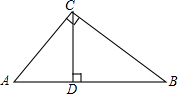
如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于D，设AC=b，BC=a，AB=c，CD=h．求证：
已知二次函数图象经过点（1，-3）、（-1，1）、（0，-2）．