题目内容
 已知AD=AE,AF=AG,AD⊥BD,AE⊥CE,求证:AB=AC.
已知AD=AE,AF=AG,AD⊥BD,AE⊥CE,求证:AB=AC.考点:全等三角形的判定与性质
专题:证明题
分析:如图,证明Rt△AEG≌Rt△ADF,得到∠EAG=∠DAF,进而得到∠EAC=∠DAB;证明△AEC≌△ADB,得到AB=AC.
解答: 证明:如图,∵AD⊥BD,AE⊥CE,
证明:如图,∵AD⊥BD,AE⊥CE,
∴∠E=∠D=90°;
在Rt△AEG与Rt△ADF中,
,
∴Rt△AEG≌Rt△ADF(HL),
∴∠EAG=∠DAF,
∴∠EAC=∠DAB;
在△AEC与△ADB中,
,
∴△AEC≌△ADB(ASA),
∴AB=AC.
 证明:如图,∵AD⊥BD,AE⊥CE,
证明:如图,∵AD⊥BD,AE⊥CE,∴∠E=∠D=90°;
在Rt△AEG与Rt△ADF中,
|
∴Rt△AEG≌Rt△ADF(HL),
∴∠EAG=∠DAF,
∴∠EAC=∠DAB;
在△AEC与△ADB中,
|
∴△AEC≌△ADB(ASA),
∴AB=AC.
点评:该题主要考查了全等三角形的判定及其性质的应用;准确找出图形中隐含的全等三角形,两次证明三角形全等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
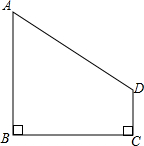 如图,在四边形ABCD中,AB⊥BC,DC⊥BC.当AB=4,DC=1,BC=4时,在BC上是否存在点P,使得AP⊥PD?若存在,求线段BP的长;若不存在,请说明理由.
如图,在四边形ABCD中,AB⊥BC,DC⊥BC.当AB=4,DC=1,BC=4时,在BC上是否存在点P,使得AP⊥PD?若存在,求线段BP的长;若不存在,请说明理由. 如图,线段AB上有一点C,且AC=2BC,D是AB中点,已知CD长为2cm,求BC、AB的长.
如图,线段AB上有一点C,且AC=2BC,D是AB中点,已知CD长为2cm,求BC、AB的长.
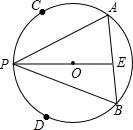 如图,已知PA、PB是⊙O的两条弦,C、D分别是
如图,已知PA、PB是⊙O的两条弦,C、D分别是
 求图中的三视图所表示的几何体的体积.
求图中的三视图所表示的几何体的体积.
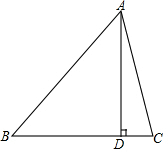 如图,在△ABC中,AD⊥BC于点D,AB=2
如图,在△ABC中,AD⊥BC于点D,AB=2