题目内容
8．在已知下列三组长度的线段中，不能构成直角三角形的是（ ）| A． | 5，12，13 | B． | 1，$\sqrt{2}$，$\sqrt{3}$ | C． | 2，3，$\sqrt{5}$ | D． | 4，5，7 |
分析 由勾股定理的逆定理，只要验证两小边的平方和是否等于最长边的平方，即可解答．
解答 解：A、52+122=132，能构成直角三角形，不符合题意；
B、$\sqrt{2}$2+12=$\sqrt{3}$2，能构成直角三角形，不符合题意；
C、22+$\sqrt{5}$2=32，能构成直角三角形，不符合题意；
D、52+42≠72，不能构成直角三角形，符合题意；
故选：D．
点评 本题考查勾股定理的逆定理的应用．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．
练习册系列答案
相关题目
19．下列计算中，正确的是（ ）
| A． | （2x+1）（2x-1）=2x2-1 | B． | （x-4）2=x2-16 | ||
| C． | （x+5）（x-6）=x2-x-30 | D． | （x+2y）2=x2+2xy+4y2 |
如图，已知AD是三角形ABC的中线，BE⊥AD，CF⊥AD交AD的延长线于点F．
3．
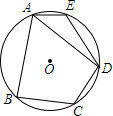如图，在⊙O的内接四边形ABCD中，AB=AD，∠C=120°，点E在弧AD上．若AE恰好为⊙O的内接正十边形的一边，弧DE的度数为（ ）
如图，在⊙O的内接四边形ABCD中，AB=AD，∠C=120°，点E在弧AD上．若AE恰好为⊙O的内接正十边形的一边，弧DE的度数为（ ）| A． | 75° | B． | 80° | C． | 84° | D． | 90° |
如图，将一长方形纸片OABC放在直角坐标系中，O为原点，C在X轴上OA=6 OC=
20．
如图，是二次函数y=ax2+bx+c图象的一部分，对称轴为直线x=-1，且过点（-4，0），给出四个结论：①abc＜0 ②2a-b=0 ③4a+2b+c＜0 ④若点（-6，y1），（3，y2）是该抛物线上的两点，则y1＞y2，其中正确的是（ ）
如图，是二次函数y=ax2+bx+c图象的一部分，对称轴为直线x=-1，且过点（-4，0），给出四个结论：①abc＜0 ②2a-b=0 ③4a+2b+c＜0 ④若点（-6，y1），（3，y2）是该抛物线上的两点，则y1＞y2，其中正确的是（ ）| A． | ①② | B． | ①②④ | C． | ②③ | D． | ②③④ |
18．计算27a8÷$\frac{1}{3}$a3÷9a2的顺序不正确的是（ ）
| A． | （27÷$\frac{1}{3}$÷9）a8-3-2 | B． | （27a8÷$\frac{1}{3}$a3）÷9a2 | C． | （27a8÷9a2）÷$\frac{1}{3}$a3 | D． | 27a8÷（$\frac{1}{3}$a3÷9a2） |