题目内容
3.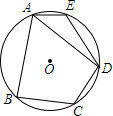 如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在弧AD上.若AE恰好为⊙O的内接正十边形的一边,弧DE的度数为( )
如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在弧AD上.若AE恰好为⊙O的内接正十边形的一边,弧DE的度数为( )| A. | 75° | B. | 80° | C. | 84° | D. | 90° |
分析 连接BD、OA、OE、OD,根据圆的内接四边形的性质得出∠BAD的度数,由AB=AD,可证得△ABD是等边三角形,求得∠ABD=60°,由圆周角定理求出∠AOD的度数,由
正十边形的性质求出∠AOE的度数,得出∠DOE的度数即可.
解答 解:连接BD、OA、OE、OD,如图所示
∵四边形ABCD是⊙O的内接四边形,
∴∠BAD+∠C=180°,
∵∠C=120°,
∴∠BAD=60°,
∵AB=AD,
∴△ABD是等边三角形,
∴∠ABD=60°,∴∠AOD=2∠ABD=120°,
∵AE恰好为⊙O的内接正十边形的一边,
∴∠AOE=$\frac{360°}{10}$=36°,
∴∠DOE=120°-36°=84°;
故选:C.
点评 此题考查了正多边形的性质、圆的内接四边形的性质、圆周角定理以及等边三角形的判定与性质.求出∠DOE的度数是解决问题的关键.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
11.下列图形是中心对称图形的有( )
①等腰三角形②等边三角形③直角三角形④正方形.
①等腰三角形②等边三角形③直角三角形④正方形.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.在已知下列三组长度的线段中,不能构成直角三角形的是( )
| A. | 5,12,13 | B. | 1,$\sqrt{2}$,$\sqrt{3}$ | C. | 2,3,$\sqrt{5}$ | D. | 4,5,7 |
15.若$\sqrt{a-1}$+$\sqrt{1-a}$=(a+b)2,则b-a=( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
12. 如图,在?ABCD中,已知AD=6cm,AB=8cm,CE平分∠BCD交BC边于点E,则AE的长为( )
如图,在?ABCD中,已知AD=6cm,AB=8cm,CE平分∠BCD交BC边于点E,则AE的长为( )
 如图,在?ABCD中,已知AD=6cm,AB=8cm,CE平分∠BCD交BC边于点E,则AE的长为( )
如图,在?ABCD中,已知AD=6cm,AB=8cm,CE平分∠BCD交BC边于点E,则AE的长为( )| A. | 2cm | B. | 4cm | C. | 6cm | D. | 8cm |