题目内容
2. 如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长与周长.
分析 (1)根据四边形EFGH是正方形,得到EH∥BC,进而得出∠AEH=∠B,∠AHE=∠C,即可判定△AEH∽△ABC;
(2)设正方形EFGH的边长为x,则DM=x,AM=30-x,根据△AEH∽△ABC,得出$\frac{EH}{BC}$=$\frac{AM}{AD}$,即$\frac{x}{40}$=$\frac{30-x}{30}$,进而解得x=$\frac{120}{7}$,即可得出正方形的边长与周长.
解答  解:(1)∵四边形EFGH是正方形,
解:(1)∵四边形EFGH是正方形,
∴EH∥BC,
∴∠AEH=∠B,∠AHE=∠C,
∴△AEH∽△ABC;
(2)如图,设AD与EH交于点M,
∵∠EFD=∠FEM=∠FDM=90°,
∴四边形EFDM是矩形,
∴EF=DM,
设正方形EFGH的边长为x,则DM=x,AM=30-x,
∵△AEH∽△ABC,
∴$\frac{EH}{BC}$=$\frac{AM}{AD}$,即$\frac{x}{40}$=$\frac{30-x}{30}$,
解得x=$\frac{120}{7}$,
∴正方形EFGH的边长为$\frac{120}{7}$cm,周长为$\frac{480}{7}$cm.
点评 本题主要考查了相似三角形的判定与性质,正方形、矩形的性质的综合应用,解决问题的关键是运用相似三角形的对应线段(对应中线、对应角平分线、对应边上的高)的比等于相似比列方程求解.

练习册系列答案
相关题目
13.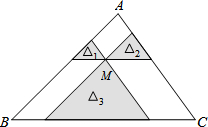 如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1,△2,△3(图中阴影部分)的面积分别是4,9和16,则△ABC的面积是( )
如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1,△2,△3(图中阴影部分)的面积分别是4,9和16,则△ABC的面积是( )
 如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1,△2,△3(图中阴影部分)的面积分别是4,9和16,则△ABC的面积是( )
如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1,△2,△3(图中阴影部分)的面积分别是4,9和16,则△ABC的面积是( )| A. | 49 | B. | 64 | C. | 100 | D. | 81 |
7.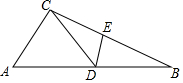 如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=60°,则∠CDE的度数为( )
如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=60°,则∠CDE的度数为( )
 如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=60°,则∠CDE的度数为( )
如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=60°,则∠CDE的度数为( )| A. | 45° | B. | 50° | C. | 51° | D. | 52° |
 如图,若∠B=28°,∠C=22°,∠A=60°,求∠BDC.
如图,若∠B=28°,∠C=22°,∠A=60°,求∠BDC.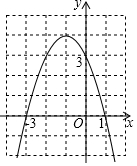 二次函数y=ax2+bx+c(a≠0)的图象如图所示,那么一元二次方程ax2+bx+c=m(a≠0,m为常数且m≤4)的两根之和为( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,那么一元二次方程ax2+bx+c=m(a≠0,m为常数且m≤4)的两根之和为( )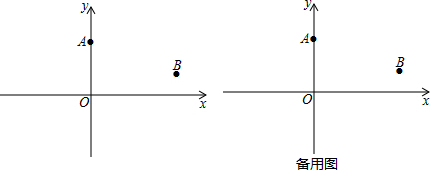
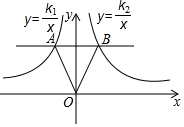 如图,在x轴上方,平行于x轴的直线与反比例函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$的图象分别交于A、B两点,连接OA、OB,若△AOB的面积为6,则k1-k2=-12.
如图,在x轴上方,平行于x轴的直线与反比例函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$的图象分别交于A、B两点,连接OA、OB,若△AOB的面积为6,则k1-k2=-12. 如图,点O为Rt△ABC斜边AB上一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD、OD.
如图,点O为Rt△ABC斜边AB上一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD、OD.