题目内容
7.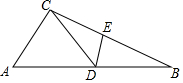 如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=60°,则∠CDE的度数为( )
如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=60°,则∠CDE的度数为( )| A. | 45° | B. | 50° | C. | 51° | D. | 52° |
分析 根据等腰三角形的性质推出∠A=∠CDA=60°,∠B=∠DCB,∠BDE=∠BED,根据三角形的外角性质求出∠B=30°,由三角形的内角和定理求出∠BDE,根据平角的定义即可求出选项.
解答 解:∵AC=CD=BD=BE,∠A=60°,
∴∠A=∠CDA=60°,∠B=∠DCB,∠BDE=∠BED,
∵∠B+∠DCB=∠CDA=60°,
∴∠B=30°,
∵∠B+∠EDB+∠DEB=180°,
∴∠BDE=∠BED=$\frac{1}{2}$(180°-30°)=75°,
∴∠CDE=180°-∠CDA-∠EDB=180°-60°-75°=45°,
故选A.
点评 本题主要考查对等腰三角形的性质,三角形的内角和定理,三角形的外角性质,邻补角的定义等知识点的理解和掌握,熟练地运用这些性质进行计算是解此题的关键.

练习册系列答案
相关题目
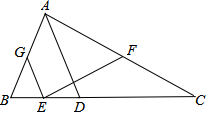 如图,在△ABC中,点D在边BC上,AB=AD,E是BD的中点,F是AC的中点.
如图,在△ABC中,点D在边BC上,AB=AD,E是BD的中点,F是AC的中点. 如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.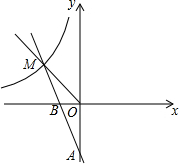 如图,一次函数y=-2x-2的图象分别交x轴、y轴于点B、A,与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第二象限交于点M,△OBM的面积是1.
如图,一次函数y=-2x-2的图象分别交x轴、y轴于点B、A,与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第二象限交于点M,△OBM的面积是1.