题目内容
17.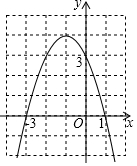 二次函数y=ax2+bx+c(a≠0)的图象如图所示,那么一元二次方程ax2+bx+c=m(a≠0,m为常数且m≤4)的两根之和为( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,那么一元二次方程ax2+bx+c=m(a≠0,m为常数且m≤4)的两根之和为( )| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
分析 利用函数图象得到抛物线与x轴的两交点坐标为(-3,0),(1,0),根据抛物线与x轴的交点问题得到ax2+bx+c=0的两根分别为x1=-3,x2=1,则根据根与相似的关系得到$\frac{b}{a}$=2,然后求一元二次方程ax2+bx+c-m=0的两根之和.
解答 解:∵抛物线与x轴的两交点坐标为(-3,0),(1,0),
∴一元二次方程ax2+bx+c=0的两根分别为x1=-3,x2=1,
∴-3+1=-$\frac{b}{a}$,即$\frac{b}{a}$=2,
∴一元二次方程ax2+bx+c-m=0的两根之和=-$\frac{b}{a}$=-2.
故选D.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.

练习册系列答案
相关题目
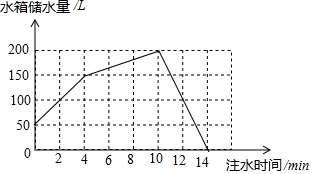 容积为200L的水箱上装有两根进水管A,B和一根排水管C.如图,先由A,B两根进水管同时向水箱内注水,再由B管单独向水箱内注水,最后由C管将水箱内的水排完.
容积为200L的水箱上装有两根进水管A,B和一根排水管C.如图,先由A,B两根进水管同时向水箱内注水,再由B管单独向水箱内注水,最后由C管将水箱内的水排完.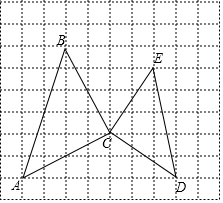 在如图10×9的网格图中,△ABC和△CDE都是等腰直角三角形,其顶点都在格点上,若点A、C的坐标分别为(-5,-2)和(-1,0).
在如图10×9的网格图中,△ABC和△CDE都是等腰直角三角形,其顶点都在格点上,若点A、C的坐标分别为(-5,-2)和(-1,0). 如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
 如图,已知△ABC,∠ABC,∠ACB的角平分线交于点O,连接AO并延长交BC于D,OH⊥BC于H,若∠BAC=60°,OH=3cm,OA长为( )cm.
如图,已知△ABC,∠ABC,∠ACB的角平分线交于点O,连接AO并延长交BC于D,OH⊥BC于H,若∠BAC=60°,OH=3cm,OA长为( )cm.