题目内容

10．若x1，x2，x3，…x10的平均数是5，x11，x12，x13，…x20的平均数是3，则x1，x2，x3，…x20的平均数是4．

分析 根据算术平均数的计算公式先求出x1+x2+x3，…+x10和x11+x12+…+x20，再计算出x1，x2，…x20的和，然后除以20，即为新数据的平均数．

解答 解：根据题意知x1+x2+x3+…+x10=10×5=50，x11+x12+x13+…+x20=10×3=30，
∴$\frac{1}{20}$（x1+x2+x3+…+x20）=$\frac{1}{20}$×（50+30）=4，
故答案为：4．

点评 此题考查了算术平均数，熟记平均数的计算公式是解决本题的关键．

练习册系列答案
相关题目
20．阅读材料：对于任何实数，我们规定符号$|\begin{array}{l}{a}&{c}\\{b}&{d}\end{array}|$的意义是$|\begin{array}{l}{a}&{c}\\{b}&{d}\end{array}|$=ad-bc．
例如：$|\begin{array}{l}{1}&{2}\\{3}&{4}\end{array}|$=1×4-2×3=-2，$|\begin{array}{l}{-2}&{4}\\{3}&{5}\end{array}|$=（-2）×5-4×3=-22．
（1）按照这个规定请你计算$|\begin{array}{l}{5}&{-4}\\{-3}&{-2}\end{array}|$的值；
（2）按照这个规定请你计算：当|x-2|=0时，$|\begin{array}{l}{3}&{7x}\\{2}&{2x-6}\end{array}|$的值．
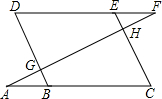1．如图所示，点E在直线DF上，点B在直线AC上，直线AF分别交BD，CE于点G，H．若∠AGB=∠EHF，∠C=∠D，请到断∠A与∠F的数量关系，并说明理由．
18．“如果一个数是整数，那么它是有理数”这个命题的条件是一个数是整数．
5．让我们来规定一种运算：$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc，例如：$|\begin{array}{l}{2}&{3}\\{4}&{5}\end{array}|$=2×5-4×3=-2，再如：$|\begin{array}{l}{x}&{2}\\{1}&{4}\end{array}|$=4x-2．按照这种运算的规定：请解答下列各个问题：
（1）$|\begin{array}{l}{-1}&{2}\\{-2}&{0.5}\end{array}|$的值为多少？
（2）x为何值时，$|\begin{array}{l}{\frac{1}{x}}&{-\frac{1}{2-x}}\\{-x}&{2}\end{array}|$=1．
15．解方程
（1）1-$\frac{2x-1}{2}$=$\frac{2x+1}{6}$
（2）$\left\{\begin{array}{l}{x+3y=4}\\{\frac{1}{4}x+\frac{1}{2}y=0}\end{array}\right.$．
2．如图，△ABC为锐角三角形，AD是BC边上的高，正方形EFGH的一边FG在BC上，顶点E、H分别在AB、AC上，已知BC=40cm，AD=30cm．
（1）求证：△AEH∽△ABC；
（2）求这个正方形的边长与周长．
19．已知a2+b2-2a-4b+5=0，求$\frac{1}{a（b+1）}$+$\frac{1}{（a+2）（b+3）}$+$\frac{1}{（a+4）（b+5）}$+…+$\frac{1}{（a+2012）（b+2013）}$的值．
20．使式子$\frac{\sqrt{2-x}}{x}$有意义的实数x的取值范围是（　　）
A．x≤2B．x＜2且x≠0C．x≤2且x≠0D．x＜2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网