题目内容
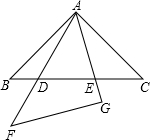 将两个全等的等腰直角三角形摆成如图所示的样子(图中所有的点、线都在同一平面内).
将两个全等的等腰直角三角形摆成如图所示的样子(图中所有的点、线都在同一平面内).(1)请在图中找出两对相似而不全等的三角形,请从其中一对说明理由.
(2)你还能再找一对相似而不全等的三角形吗?请说明理由.
考点:相似三角形的判定,等腰直角三角形
专题:
分析:(1)由于△BAC和△AGF都是等腰直角三角形,因此∠B=∠AFG=45°,可得出∠BAE=∠ADE=45°+∠BAD;已知了△EAD和△EBA中,∠AED是公共角,可得出两三角形相似;
(2)由(1)可证得△BAE∽△CDA.
(2)由(1)可证得△BAE∽△CDA.
解答:解:(1)△ADE∽△BAE,△CDA∽△ADE.
∵△BAC和△AGF都是等腰直角三角形,
∴∠B=∠AFG=45°,
∴∠BAE=∠ADE=45°+∠BAD;
∵△EAD和△EBA中,∠AED是公共角,
∴△ADE∽△BAE;
同理,可得△CDA∽△ADE.
(2)△BAE∽△CDA,
∵△ADE∽△BAE,△CDA∽△ADE.
∴△BAE∽△CDA.
∵△BAC和△AGF都是等腰直角三角形,
∴∠B=∠AFG=45°,
∴∠BAE=∠ADE=45°+∠BAD;
∵△EAD和△EBA中,∠AED是公共角,
∴△ADE∽△BAE;
同理,可得△CDA∽△ADE.
(2)△BAE∽△CDA,
∵△ADE∽△BAE,△CDA∽△ADE.
∴△BAE∽△CDA.
点评:此题考查了相似三角形的判定以及等腰直角三角形性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
某天,5个同学去打羽毛球,从上午8:55一直到11:55,若这段时间内,一直玩双打(即须4人同时上场),则平均一个人的上场时间为几分钟?( )
| A、36 | B、45 |
| C、135 | D、144 |
把抛物线y=-x2向右平移一个单位,再向上平移3个单位,得到抛物线的解析式为( )
| A、y=-(x-1)2+3 |
| B、y=(x-1)2+3 |
| C、y=-(x+1)2+3 |
| D、y=(x+1)2+3 |
 如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于点O,OB=OC.求证:∠BAO=∠CAO.
如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于点O,OB=OC.求证:∠BAO=∠CAO.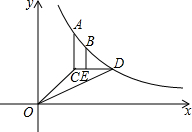 如图,已知反比例函数y=
如图,已知反比例函数y= 如图,△ABC和△ADC都是等边三角形.
如图,△ABC和△ADC都是等边三角形.