题目内容
分别写出满足下列条件的一元二次方程各至少一个:
(1)有一个根为0;(2)有一个根为1;(3)有一个根为-1;(4)两根相等;(5)两根互为相反数;(6)两根互为倒数;(7)无实数根.
(1)有一个根为0;(2)有一个根为1;(3)有一个根为-1;(4)两根相等;(5)两根互为相反数;(6)两根互为倒数;(7)无实数根.
考点:根与系数的关系,一元二次方程的解,根的判别式
专题:开放型
分析:(1)写出的方程两根之积为0;
(2)写出的方程满足x=1;
(3)写出的方程满足x=-1;
(4)写出的方程的判别式的值为0;
(5)写出的方程两根之和为0;
(6)写出的方程两根之积为1;
(7)写出的方程的判别式的值小于0.
(2)写出的方程满足x=1;
(3)写出的方程满足x=-1;
(4)写出的方程的判别式的值为0;
(5)写出的方程两根之和为0;
(6)写出的方程两根之积为1;
(7)写出的方程的判别式的值小于0.
解答:解:(1)x2-x=0;
(2)x2-x=0;
(3)x2+x=0;
(4)x2=0;
(5)x2-1=0;
(6)x2-3x+1=0;
(7)x2+2=0.
(2)x2-x=0;
(3)x2+x=0;
(4)x2=0;
(5)x2-1=0;
(6)x2-3x+1=0;
(7)x2+2=0.
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.也考查了根的判别式.
| b |
| a |
| c |
| a |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在Rt△ABC中,∠C=90°,则tanA•tanB等于( )
| A、0 | B、1 | C、-1 | D、不确定 |
若a,b是一元二次方程x2+2x-1=0的两根,则下列说法正确的是( )
| A、a+b=2 |
| B、a+b=-1 |
| C、ab=-1 |
| D、ab=1 |
若
与
化成最简二次根式是可以合并的,则m、n的值为( )
| m+n | 4n |
| 27m+9n |
| A、m=0,n=2 |
| B、m=1,n=1 |
| C、m=0,n=2或m=1,n=1 |
| D、m=2,n=0 |
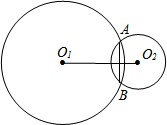 ⊙O1和⊙O2相交于A、B两点,⊙O1的半径为5cm,⊙O2的半径为3
⊙O1和⊙O2相交于A、B两点,⊙O1的半径为5cm,⊙O2的半径为3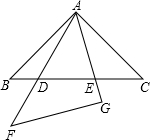 将两个全等的等腰直角三角形摆成如图所示的样子(图中所有的点、线都在同一平面内).
将两个全等的等腰直角三角形摆成如图所示的样子(图中所有的点、线都在同一平面内).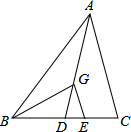 如图,△ABC中,AD为BC边上的中线,点G是△ABC的重心,GE∥AC,求S△GDE:S△GBD.
如图,△ABC中,AD为BC边上的中线,点G是△ABC的重心,GE∥AC,求S△GDE:S△GBD.