题目内容
 如图,△ABC和△ADC都是等边三角形.
如图,△ABC和△ADC都是等边三角形.(1)AB与CD是否平行?为什么?
(2)连结BD,BD与AC是否垂直?为什么?
考点:菱形的判定与性质,等边三角形的性质
专题:
分析:(1)利用等边三角形的性质得到∠BAC=∠ACD=60°,则“内错角相等,两直线平行”;
(2)欲证明BD与AC垂直,只需证得四边形ABCD是菱形.
(2)欲证明BD与AC垂直,只需证得四边形ABCD是菱形.
解答: 解:(1)AB与CD平行.理由如下:
解:(1)AB与CD平行.理由如下:
∵△ABC和△ADC都是等边三角形,
∴∠BAC=∠ACD=60°,
∴AB∥CD;
(2)BD与AC垂直.理由如下:
∵△ABC和△ADC都是等边三角形,
∴∠DAC=∠ACB=60°,AB=BC
∴AD∥BC.
又∵由(1)知,AB∥CD,
∴四边形ABCD是平行四边形.
又∵AB=BC,
∴平行四边形ABCD是菱形,
∴BD⊥AC,即BD与AC垂直.
 解:(1)AB与CD平行.理由如下:
解:(1)AB与CD平行.理由如下:∵△ABC和△ADC都是等边三角形,
∴∠BAC=∠ACD=60°,
∴AB∥CD;
(2)BD与AC垂直.理由如下:
∵△ABC和△ADC都是等边三角形,
∴∠DAC=∠ACB=60°,AB=BC
∴AD∥BC.
又∵由(1)知,AB∥CD,
∴四边形ABCD是平行四边形.
又∵AB=BC,
∴平行四边形ABCD是菱形,
∴BD⊥AC,即BD与AC垂直.
点评:本题考查了菱形的判定与性质、等边三角形的性质.此题利用了“邻边相等的平行四边形为菱形”推知四边形ABCD是菱形.

练习册系列答案
相关题目
已知一元二次方程ax2+bx+c=0(a≠0)的一根是另一个根的
,则a、b、c的关系正确的是( )
| 1 |
| 4 |
| A、5ac=4b2 |
| B、25b2=25ac |
| C、4b2=25ac |
| D、4b2=-25ac |
若a,b是一元二次方程x2+2x-1=0的两根,则下列说法正确的是( )
| A、a+b=2 |
| B、a+b=-1 |
| C、ab=-1 |
| D、ab=1 |
下列方程中两根互为倒数有( )
①x2-2x-1=0;②2x2-7x+2=0;③x2-x+1=0.
①x2-2x-1=0;②2x2-7x+2=0;③x2-x+1=0.
| A、0个 | B、1个 | C、2个 | D、3个 |
一元二次方程x2-x+2=0的根的情况是( )
| A、无实数根 |
| B、有两个不相等的实数根 |
| C、有两个相等的实数根 |
| D、无法确定 |

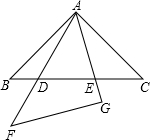 将两个全等的等腰直角三角形摆成如图所示的样子(图中所有的点、线都在同一平面内).
将两个全等的等腰直角三角形摆成如图所示的样子(图中所有的点、线都在同一平面内).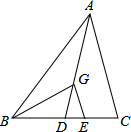 如图,△ABC中,AD为BC边上的中线,点G是△ABC的重心,GE∥AC,求S△GDE:S△GBD.
如图,△ABC中,AD为BC边上的中线,点G是△ABC的重心,GE∥AC,求S△GDE:S△GBD.