题目内容
如图，CD⊥AB，BE⊥AC，垂足分别为D、E，BE、CD相交于点O，OB=OC．求证：∠BAO=∠CAO．考点：全等三角形的判定与性质
专题：证明题
分析：由条件可先证明△BOD≌△COE，可得OD=OE，则可证得△AOD≌△AOE，则可得结论．
解答：证明：∵CD⊥AB，BE⊥AC，
∴∠BDO=∠CEO．
在△BOD和△COE中
，
∴△BOD≌△COE，
∴OD=OE．
在Rt△AOD和Rt△AOE中
，
∴△AOD≌△AOE，
∴∠BAO=∠CAO．
∴∠BDO=∠CEO．
在△BOD和△COE中
|
∴△BOD≌△COE，
∴OD=OE．
在Rt△AOD和Rt△AOE中
|
∴△AOD≌△AOE，
∴∠BAO=∠CAO．
点评：本题主要考查三角形全等的判定和性质，利用三角形全等来找条件是解本题的关键．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
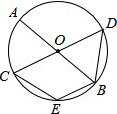已知AB、CD是⊙O的两条直径，CE∥AB，求证：
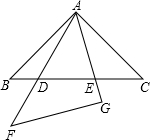将两个全等的等腰直角三角形摆成如图所示的样子（图中所有的点、线都在同一平面内）．