题目内容
2.下列四组线段中,能组成直角三角形的是( )| A. | a=1,b=2,c=3 | B. | a=4,b=2,c=3 | C. | a=4,b=2,c=5 | D. | a=4,b=5,c=3 |
分析 利用勾股定理的逆定理:如果三角形两条边的平方和等于第三边的平方,那么这个三角形就是直角三角形.最长边所对的角为直角.由此判定即可.
解答 解:A、因为1+2=3,所以三条线段不能组成三角形,一定不能组成直角三角形;
B、因为22+32≠42,所以三条线段不能组成直角三角形;
C、因为22+42≠52,所以三条线段不能组成直角三角形;
D、因为42+32=52,所以三条线段能组成直角三角形.
故选:D.
点评 此题考查勾股定理逆定理的运用;熟记两条短边的平方和等于长边的平方是直角三角形是解决问题的关键.

练习册系列答案
相关题目
12.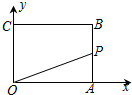 如图,在矩形OABC中,已知A(6,0),C(0,4),动点P从点A出发,沿A-B-C-O的路线匀速运动,设动点P的运动时间为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )
如图,在矩形OABC中,已知A(6,0),C(0,4),动点P从点A出发,沿A-B-C-O的路线匀速运动,设动点P的运动时间为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )
 如图,在矩形OABC中,已知A(6,0),C(0,4),动点P从点A出发,沿A-B-C-O的路线匀速运动,设动点P的运动时间为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )
如图,在矩形OABC中,已知A(6,0),C(0,4),动点P从点A出发,沿A-B-C-O的路线匀速运动,设动点P的运动时间为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )| A. | 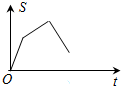 | B. | 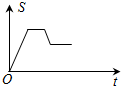 | C. |  | D. |  |
14.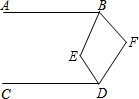 如图,已知AB∥CD,∠EBF=2∠ABE,∠EDF=2∠CDE,则∠E与∠F之间满足的数量关系是( )
如图,已知AB∥CD,∠EBF=2∠ABE,∠EDF=2∠CDE,则∠E与∠F之间满足的数量关系是( )
 如图,已知AB∥CD,∠EBF=2∠ABE,∠EDF=2∠CDE,则∠E与∠F之间满足的数量关系是( )
如图,已知AB∥CD,∠EBF=2∠ABE,∠EDF=2∠CDE,则∠E与∠F之间满足的数量关系是( )| A. | ∠E=∠F | B. | ∠E+∠F=180° | C. | 3∠E+∠F=360° | D. | 2∠E-∠F=90° |
 平面直角坐标系中,线段AB端点的坐标分别为A(-2,0),B(0,2),平移后,点A的对应点A′的坐标为A′(0,-1),则点B的对应点B′的坐标为(2,1).线段AB平移的距离为$\sqrt{5}$.
平面直角坐标系中,线段AB端点的坐标分别为A(-2,0),B(0,2),平移后,点A的对应点A′的坐标为A′(0,-1),则点B的对应点B′的坐标为(2,1).线段AB平移的距离为$\sqrt{5}$.