题目内容
13. 平面直角坐标系中,线段AB端点的坐标分别为A(-2,0),B(0,2),平移后,点A的对应点A′的坐标为A′(0,-1),则点B的对应点B′的坐标为(2,1).线段AB平移的距离为$\sqrt{5}$.
平面直角坐标系中,线段AB端点的坐标分别为A(-2,0),B(0,2),平移后,点A的对应点A′的坐标为A′(0,-1),则点B的对应点B′的坐标为(2,1).线段AB平移的距离为$\sqrt{5}$.
分析 先利用点A和点A′的坐标特征得到平移的方向与距离,然后利用此平移规律确定B′点的坐标,再利用勾股定理计算线段AB平移的距离.
解答 解:点A(-2,0)先向右平移2个单位,再向下平移1个单位得到点A′(0,-1),
所以点B(0,2)向右平移2个单位,再向下平移1个单位得到点B′(2,1),
线段AB平移的距离=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$.
故答案为(2,1),$\sqrt{5}$.
点评 本题考查了坐标与图形变化-平移:在平面直角坐标系内,把一个图形各个点的横坐标都加上(或减去)一个整数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;如果把它各个点的纵坐标都加(或减去)一个整数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
3.在数轴上表示-3和2016的点之间的距离是( )
| A. | 2016 | B. | 2013 | C. | 2019 | D. | -2019 |
4.下列说法正确的是( )
| A. | 求sin30°的按键顺序是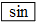 、30、= 、30、= | |
| B. | 求23的按键顺序 、2、 、2、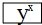 、3、= 、3、= | |
| C. | 求$\sqrt{8}$的按键顺序是 、 、 、8、= 、8、= | |
| D. | 已知sinA=0.5018,用计算器求锐角A的大小,按键顺序是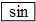 、 、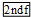 、0.5018、= 、0.5018、= |
8.下列汽车标志中,不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
2.下列四组线段中,能组成直角三角形的是( )
| A. | a=1,b=2,c=3 | B. | a=4,b=2,c=3 | C. | a=4,b=2,c=5 | D. | a=4,b=5,c=3 |
3.在四边形ABCD中,AB=DC,AD=BC,请再添加一个条件,使四边形ABCD是矩形.添加的条件不能是( )
| A. | AB∥DC | B. | ∠A=90° | C. | ∠B=90° | D. | AC=BD |
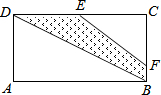 如图,矩形ABCD中,AB=8cm,BC=4cm,E是DC的中点,BF=$\frac{1}{4}$BC,则四边形DBFE的面积为( )
如图,矩形ABCD中,AB=8cm,BC=4cm,E是DC的中点,BF=$\frac{1}{4}$BC,则四边形DBFE的面积为( )