Question

2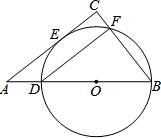．如图，在Rt△ACB中，∠C=90°，D是AB上一点，以BD为直径的⊙O切AC于点E，交BC于点F，连接DF．
（1）求证：DF=2CE；
（2）若BC=3，sinB=$\frac{4}{5}$，求线段BF的长．

Answer 1

分析 （1）连接OE交DF于G，首先证明四边形EGFC是矩形，再根据垂径定理即可证明．
（2）设OE=x，由OE∥BC，得△AOE∽△ABC，得$\frac{OE}{BC}=\frac{AO}{AB}$，列出方程求出x，再在Rt△BDF中，由sinB=$\frac{4}{5}$，推出cosB=$\frac{3}{5}$=$\frac{BF}{BD}$，即可解决问题．

解答 （1）证明：连接OE交DF于G，
∵AC切⊙O于E，
∴∠CEO=90°．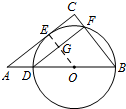
又∵BD为⊙O的直径，
∴∠DFC=∠DFB=90°．
∵∠C=90°，
∴四边形CEGF为矩形．
∴CE=GF，∠EGF=90°，
∴DF=2CE．
（2）解：在Rt△ABC中，∵∠C=90°，BC=3，$sinB=\frac{4}{5}$，
∴AB=5，
设OE=x，∵OE∥BC，
∴△AOE∽△ABC．
∴$\frac{OE}{BC}=\frac{AO}{AB}$，
∴$\frac{x}{3}=\frac{5-x}{5}$，
∴$x=\frac{15}{8}$，
∴BD=$\frac{15}{4}$．
在Rt△BDF中，∵∠DFB=90°，sinB=$\frac{4}{5}$，
∴cosB=$\frac{3}{5}$=$\frac{BF}{BD}$=$\frac{BF}{\frac{15}{4}}$，
∴BF=$\frac{9}{4}$．

点评 本题考查切线的性质、矩形的判定和性质、垂径定理、三角函数等知识，解题的关键是灵活运用这些知识解决问题，属于中考常考题型．