题目内容
1.在等腰△ABC中,CA=CB,点D,E在射线AB上,不与A,B重合(D在E的左边),且∠DCE=$\frac{1}{2}$∠ACB.(1)如图1,若∠ACB=90°,将△CAD沿CD翻折,点A与M重合,求证:△MCE≌△BCE;
(2)如图2,若∠ACB=120°,且以AD、DE、EB为边的三角形是直角三角形,求$\frac{AD}{EB}$的值;
(3)∠ACB=120°,点D在射线AB上运动,AC=3,则AD的取值范围为0<AD<2$\sqrt{3}$.
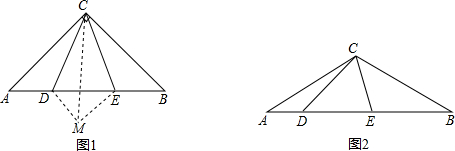
分析 (1)由对折得到∠A=∠CMD=45°=∠B,∠ACD=∠MCD,CM=AC=BC,再判断出BC=CM,即可;
(2)先求出∠DME=∠A+∠B=60°,再分两种情况利用锐角三角函数即可;
(3)先判断出AD最长时的位置,然后用锐角三角函数计算即可.
解答 证明:(1)∵△CMD是△CAD对折所得,
∴∠A=∠CMD=45°=∠B,∠ACD=∠MCD,CM=AC=BC
∵∠DCE=$\frac{1}{2}$∠ACB=45°,
∴∠MCD+∠MCE=45°,
∴∠ACD+∠MCE=45°
∵∠ACD+∠BCE=45°,
∴∠MCE=∠BCE,
∵AC=BC,
∴BC=CM,
在△MCE和△BCE中
$\left\{\begin{array}{l}{∠MCE=∠BCE}\\{CM=CB}\\{∠CME=∠B}\end{array}\right.$,
∴△MCE≌△BCE,
(2)如图,
∵AC=BC,∠ACB=120°,
∴∠A=∠B=30°,
同(1)方法可证,△CME≌△CBE,
∴∠CME=∠B,
∴∠DME=∠A+∠B=60°,
∵AD、DE、EB为边的三角形是直角三角形,
∴△DME是直角三角形,
∴∠MDE=90°,或∠DEM=90°,
①当∠MDE=90°时,∠DEM=30°,
∴sin∠DEM=$\frac{DM}{ME}$,
∴$\frac{DM}{ME}=\frac{1}{2}$,
∴$\frac{AD}{EB}=\frac{1}{2}$,
②当∠DEM=90°时,∠MDE=30°,
∴sin∠MDE=$\frac{EM}{DM}$,
∴$\frac{EM}{DM}=\frac{1}{2}$,
∴$\frac{BE}{AD}=\frac{1}{2}$,
∴$\frac{AD}{BE}$=2,
即:$\frac{AD}{BE}$=$\frac{1}{2}$或2;
(3)∵D在E的左边,
∴AD最大只能靠近AB边上的高,
∵∠ACB=120°,AC=3,
∴AB边上的高为2$\sqrt{3}$,
∴0<AD<2$\sqrt{3}$.
故答案为0<AD<2$\sqrt{3}$.
点评 此题是几何变换综合题,主要考查了对折的性质,全等三角形的判定和性质,直角三角形的判定,锐角三角函数的意义,解本题的关键是判断△CME≌△CBE.

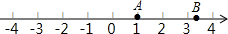 如图,在数轴上表示A,B两点对应的数分别是1,$\sqrt{10}$,则点B关于点A的对称点表示的数是( )
如图,在数轴上表示A,B两点对应的数分别是1,$\sqrt{10}$,则点B关于点A的对称点表示的数是( )| A. | -$\sqrt{10}$ | B. | -1-$\sqrt{10}$ | C. | $\sqrt{10}$-2 | D. | 2-$\sqrt{10}$ |
| A. | 2a8 | B. | 2a9 | C. | 4a8 | D. | 4a9 |
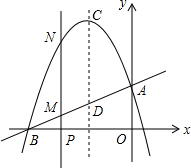 如图,已知直线y=$\frac{1}{2}$x+$\frac{7}{2}$与x轴、y轴分别相交于B、A两点,抛物线y=ax2+bx+c经过A、B两点,且对称轴为x=-3.
如图,已知直线y=$\frac{1}{2}$x+$\frac{7}{2}$与x轴、y轴分别相交于B、A两点,抛物线y=ax2+bx+c经过A、B两点,且对称轴为x=-3.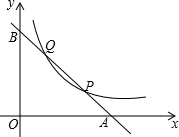 如图,直线y=-x+3与x,y轴分别交于点A,B.与反比例函数y=$\frac{k}{x}$的图象交于点P和点Q,若PQ=2$\sqrt{2}$,则k=$\frac{5}{4}$.
如图,直线y=-x+3与x,y轴分别交于点A,B.与反比例函数y=$\frac{k}{x}$的图象交于点P和点Q,若PQ=2$\sqrt{2}$,则k=$\frac{5}{4}$.
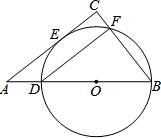 如图,在Rt△ACB中,∠C=90°,D是AB上一点,以BD为直径的⊙O切AC于点E,交BC于点F,连接DF.
如图,在Rt△ACB中,∠C=90°,D是AB上一点,以BD为直径的⊙O切AC于点E,交BC于点F,连接DF. a、b、c三点在数轴上的位置如图所示,化简$\sqrt{{a}^{2}}$-|a+b|+$\sqrt{{b}^{2}-2bc+{c}^{2}}$.
a、b、c三点在数轴上的位置如图所示,化简$\sqrt{{a}^{2}}$-|a+b|+$\sqrt{{b}^{2}-2bc+{c}^{2}}$.