题目内容
6.计算(x2-4x+n)(x2+mx+8)的结果不含x2和x3的项,那么m+n=12.分析 先用多项式乘以多项式的运算法则展开求它们的积,并且把m、n看作常数合并关于x的同类项,令x2及x3的系数为0,构造关于m、n的二元一次方程组,求出m、n的值即可得答案.
解答 解:(x2-4x+n)(x2+mx+8)=x4+(m-4)x3+(8+n-4m)x2+(mn-32)x+8n,
又∵结果不含x2和x3的项,
∴$\left\{\begin{array}{l}{m-4=0}\\{8+n-4m=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=4}\\{n=8}\end{array}\right.$.
∴m+n=12,
故答案为:12.
点评 本题主要考查了多项式乘多项式的运算,当多项式中不含有哪一项时,即哪一项的系数为0.

练习册系列答案
相关题目
1.计算(-a+b)(a-b)等于( )
| A. | a2-b2 | B. | -a2+b2 | C. | -a2-2ab+b2 | D. | -a2+2ab-b2 |
11.计算(2a3)2•a3的结果是( )
| A. | 2a8 | B. | 2a9 | C. | 4a8 | D. | 4a9 |
18.若x2-3x-6=0,则2x2-6x-6的值为( )
| A. | -8 | B. | 14 | C. | 6 | D. | -2 |
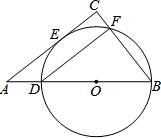 如图,在Rt△ACB中,∠C=90°,D是AB上一点,以BD为直径的⊙O切AC于点E,交BC于点F,连接DF.
如图,在Rt△ACB中,∠C=90°,D是AB上一点,以BD为直径的⊙O切AC于点E,交BC于点F,连接DF.