题目内容
17.一艘渔船向正东航行,渔船上的渔民在A处看见灯塔M在北偏东60°方向,且相距14$\sqrt{3}$km,一段时间后到达B处,在B处看见灯塔M在北偏东30°方向,此时,灯塔M与渔船的距离是( )| A. | 7$\sqrt{2}$km | B. | 14$\sqrt{2}$km | C. | 7km | D. | 14km |
分析 作BH⊥AM于H,根据题意标注方向角,根据等腰三角形的性质和锐角三角函数的概念进行计算即可.
解答 解:如图,作BH⊥AM于H,
由题意得,∠MAB=30°,∠MBC=60°,
∴∠M=30°,
∴BM=BA,又BH⊥AM,
∴MH=$\frac{1}{2}$AM=7$\sqrt{3}$,又∠M=30°,
∴BM=$\frac{MH}{cos30°}$=14km,
故选:D.
点评 本题考查的是解直角三角形的应用-方向角问题,正确画出图形、准确标注方向角、掌握锐角三角函数的概念是解题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
2.两相似三角形的面积之比为4:9,周长和是20cm,那么较小的三角形的周长是( )
| A. | 4cm | B. | 7cm | C. | 8cm | D. | 9cm |
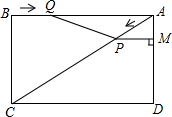 已知:如图,在矩形ABCD中,AC是对角线,AB=4cm,BC=3cm.点P从点A出发,沿AC方向匀速运动,速度为1cm/s,同时,点Q从点B出发,沿BA方向匀
已知:如图,在矩形ABCD中,AC是对角线,AB=4cm,BC=3cm.点P从点A出发,沿AC方向匀速运动,速度为1cm/s,同时,点Q从点B出发,沿BA方向匀