题目内容
7.已知:3xn+3+m-n=3p与x2-m-3m+2np=-1都是关于x的一元一次方程,且它们的解互为相反数,求m、n分别是多少?关于x的方程$\frac{x-1}{5}$+p=1的解是多少?分析 首先根据一元一次方程的定义可得n=-2,m=1,把n、m的值代入3xn+3+m-n=3p与x2-m-3m+2np=-1计算出x的值,再根据它们的解互为相反数可得到p-1+2+4p=0,计算出p的值,然后再解方程$\frac{x-1}{5}$+p=1即可.
解答 解:由题意得:n+3=1,2-m=1,
解得:n=-2,m=1,
把n=-2,m=1代入3xn+3+m-n=3p与x2-m-3m+2np=-1可得:
3x+1+2=3p,x-3-4p=-1,
解x+1+2=3p得x=p-1,
解x-3-4p=-1得x=2+4p,
∵它们的解互为相反数,
∴p-1+2+4p=0,
解得:p=-$\frac{1}{5}$,
把p=-$\frac{1}{5}$代入$\frac{x-1}{5}$+p=1得$\frac{x-1}{5}$-$\frac{1}{5}$=1,
解得x=7.
点评 此题主要考查了一元一次方程的定义,以及一元一次方程的解法,关键是正确确定m、n的值.

练习册系列答案
相关题目
17.一艘渔船向正东航行,渔船上的渔民在A处看见灯塔M在北偏东60°方向,且相距14$\sqrt{3}$km,一段时间后到达B处,在B处看见灯塔M在北偏东30°方向,此时,灯塔M与渔船的距离是( )
| A. | 7$\sqrt{2}$km | B. | 14$\sqrt{2}$km | C. | 7km | D. | 14km |
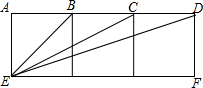 如图由三个边长为1正方形拼成矩形AEFD,求证:△BCE∽△BED.
如图由三个边长为1正方形拼成矩形AEFD,求证:△BCE∽△BED.