题目内容
1.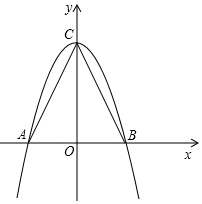 如图,在△ABC中,AB=2,AC=BC=$\sqrt{5}$
如图,在△ABC中,AB=2,AC=BC=$\sqrt{5}$(1)以AB所在的直线为x轴,AB的垂直平分线为y轴,建立直角坐标系如图,请你分别写出A、B、C三点的坐标;
(2)求过A、B、C三点且以C为顶点的抛物线的解析式;
(3)若D为抛物线上的一动点,当D点坐标为何值时,S△ABD=$\frac{1}{2}$S△ABC.
分析 (1)根据等腰三角形“三线合一”的性质求得点A、B的坐标;在直角△OAC中,利用勾股定理来求点C的坐标;
(2)因为对称轴是y轴,故设抛物线的解析式是:y=ax2+b.把点B、C的坐标分别代入函数解析式,借用方程组求得系数的值即可;
(3)△ABD与△ABC是同底等高的两个三角形,由此求得点D的纵坐标,结合二次函数图象上点的坐标特征来求点D的横坐标即可.
解答 解:(1)∵AB的垂直平分线为y轴,
∴OA=OB=$\frac{1}{2}$AB=$\frac{1}{2}$×2=1,
∴A的坐标是(-1,0),B的坐标是(1,0).
在直角△OAC中,OC=$\sqrt{B{C}^{2}-O{B}^{2}}$=2,
则C的坐标是:(0,2);
(2)设抛物线的解析式是:y=ax2+b.
根据题意得:$\left\{\begin{array}{l}{a+b=2}\\{b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-2}\\{b=2}\end{array}\right.$,
则抛物线的解析式是:y=-2x2+2;
(3)∵S△ABC=$\frac{1}{2}$AB•OC=$\frac{1}{2}$×2×2=2,
∴S△ABD=$\frac{1}{2}$S△ABC=1.
设D的纵坐标是m,则$\frac{1}{2}$AB•|m|=1,
则m=±1.
当m=1时,-2x2+2=1,解得:x=±$\frac{\sqrt{2}}{2}$,
当m=-1时,-2x2+2=-1,解得:x=±$\frac{\sqrt{6}}{2}$,
则D的坐标是:($\frac{\sqrt{2}}{2}$,1)或(-$\frac{\sqrt{2}}{2}$,1)或($\frac{\sqrt{6}}{2}$,-1),或(-$\frac{\sqrt{6}}{2}$,-1).
点评 本题考查了二次函数综合题.解题时,需要综合利用等腰三角形的性质,坐标与图形性质,三角形的面积公式,待定系数法求二次函数解析式以及二次函数图象上点的坐标特征,综合性比较强,注意“数形结合”数学思想的应用.

| A. | y=(x+2)2+4 | B. | y=(x-2)2-4 | C. | y=(x-2)2+4 | D. | y=(x+2)2-4 |
| A. | 3a | B. | a3 | C. | 2a2 | D. | 2a3 |
| A. | (-1,1) | B. | (-2,6) | C. | (2,4) | D. | (4,-1) |
| 甲 | 乙 | 丙 | |
| $\overline{x}$ | 8 | 9 | |
| s2 | 1 | 1.2 |
| A. | $\overline x=8$,S2=0.7 | B. | $\overline x=8$,S2=1.2 | C. | $\overline x=9$,S2=1 | D. | $\overline x=9$,S2=1.5 |
 如图,△ABC中,点D在边AB上,满足∠ACD=∠ABC,若AC=$\sqrt{3}$,AD=1,求DB的长.
如图,△ABC中,点D在边AB上,满足∠ACD=∠ABC,若AC=$\sqrt{3}$,AD=1,求DB的长.
 如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线于点F,若S△DEC=9,则S△BCF=( )
如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线于点F,若S△DEC=9,则S△BCF=( )