题目内容
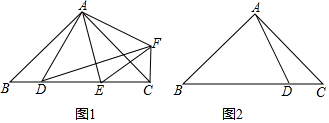
10. 如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线于点F,若S△DEC=9,则S△BCF=( )
如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线于点F,若S△DEC=9,则S△BCF=( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
分析 根据平行四边形的性质得到AD∥BC和△DEF∽△BCF,由已知条件求出△DEF的面积,根据相似三角形的面积比是相似比的平方得到答案.
解答 解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△DEF∽△BCF,
∴$\frac{EF}{CF}$=$\frac{DE}{BC}$,$\frac{{S}_{△DEF}}{{S}_{△BCF}}$=($\frac{DE}{BC}$)2,
∵E是边AD的中点,
∴DE=$\frac{1}{2}$AD=$\frac{1}{2}$BC,
∴$\frac{EF}{CE}$=$\frac{1}{2}$,
∴△DEF的面积=$\frac{1}{3}$S△DEC=3,
∴S△BCF=12;
故选D.
点评 本题考查的是平行四边形的性质、相似三角形的判定和性质;掌握三角形相似的判定定理和性质定理是解题的关键,注意:相似三角形的面积比是相似比的平方.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
20.下列运算正确的是( )
| A. | 2a+3b=5ab | B. | (3a3)2=6a6 | C. | a6÷a2=a3 | D. | a2•a3=a5 |
18. 如图,正方形ABCD边长为2,AB∥x轴,AD∥y轴,顶点A恰好落在双曲线y=$\frac{1}{2x}$上,边CD,BC分别交双曲线于E,F两点,若线段AE过原点,则EF的长为( )
如图,正方形ABCD边长为2,AB∥x轴,AD∥y轴,顶点A恰好落在双曲线y=$\frac{1}{2x}$上,边CD,BC分别交双曲线于E,F两点,若线段AE过原点,则EF的长为( )
 如图,正方形ABCD边长为2,AB∥x轴,AD∥y轴,顶点A恰好落在双曲线y=$\frac{1}{2x}$上,边CD,BC分别交双曲线于E,F两点,若线段AE过原点,则EF的长为( )
如图,正方形ABCD边长为2,AB∥x轴,AD∥y轴,顶点A恰好落在双曲线y=$\frac{1}{2x}$上,边CD,BC分别交双曲线于E,F两点,若线段AE过原点,则EF的长为( )| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{\sqrt{13}}{3}$ | D. | $\frac{4}{3}$ |
5. 如图,AD是⊙O的切线,切点为A,AC是⊙O的直径,CD交⊙O于点B,连接OB,若$\widehat{AB}$的度数为70°,则∠D的大小为( )
如图,AD是⊙O的切线,切点为A,AC是⊙O的直径,CD交⊙O于点B,连接OB,若$\widehat{AB}$的度数为70°,则∠D的大小为( )
 如图,AD是⊙O的切线,切点为A,AC是⊙O的直径,CD交⊙O于点B,连接OB,若$\widehat{AB}$的度数为70°,则∠D的大小为( )
如图,AD是⊙O的切线,切点为A,AC是⊙O的直径,CD交⊙O于点B,连接OB,若$\widehat{AB}$的度数为70°,则∠D的大小为( )| A. | 70° | B. | 60° | C. | 55° | D. | 35° |
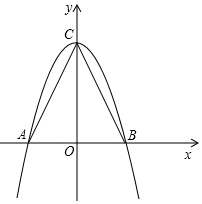 如图,在△ABC中,AB=2,AC=BC=$\sqrt{5}$
如图,在△ABC中,AB=2,AC=BC=$\sqrt{5}$ (一)知识拓展
(一)知识拓展