题目内容
11.甲、乙、丙三名运动员参加了射击预选赛,他们射击的平均环数$\overline{x}$及其方差s2如表所示.需要选一个成绩较好且状态稳定的人去参赛,如果选定的是乙,则乙的情况应为( )| 甲 | 乙 | 丙 | |
| $\overline{x}$ | 8 | 9 | |
| s2 | 1 | 1.2 |
| A. | $\overline x=8$,S2=0.7 | B. | $\overline x=8$,S2=1.2 | C. | $\overline x=9$,S2=1 | D. | $\overline x=9$,S2=1.5 |
分析 根据平均数和方差的意义即可得出答案.
解答 解:∵需要选一个成绩较好且状态稳定的人去参赛,
∴乙的平均成绩要高,且方差要小,
故选:C.
点评 本题主要考查平均数和方差,熟练掌握平均数和方差的意义是解题的关键.

练习册系列答案
相关题目
6.若a<$\sqrt{11}$<b,且a,b为两个连续的正整数,则a+b等于( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
16.分式$\frac{{x}^{2}-1}{x-1}$的值为0,则x的值为( )
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
3. 如图,⊙O是△ABC的外接圆,若∠AOB=110°,则∠ACB的度数是( )
如图,⊙O是△ABC的外接圆,若∠AOB=110°,则∠ACB的度数是( )
 如图,⊙O是△ABC的外接圆,若∠AOB=110°,则∠ACB的度数是( )
如图,⊙O是△ABC的外接圆,若∠AOB=110°,则∠ACB的度数是( )| A. | 55° | B. | 70° | C. | 125° | D. | 110° |
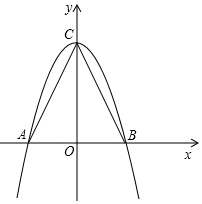 如图,在△ABC中,AB=2,AC=BC=$\sqrt{5}$
如图,在△ABC中,AB=2,AC=BC=$\sqrt{5}$ (一)知识拓展
(一)知识拓展