题目内容
 如图,∠DAE=∠EAF,∠BAD=∠CAF,则下列结论:①AD平分∠BAF;②AF平分∠DAC;③AE平分∠DAF;④AF平分∠EAC;⑤AE平分∠BAC,正确的有
如图,∠DAE=∠EAF,∠BAD=∠CAF,则下列结论:①AD平分∠BAF;②AF平分∠DAC;③AE平分∠DAF;④AF平分∠EAC;⑤AE平分∠BAC,正确的有考点:三角形的角平分线、中线和高
专题:
分析:由∠DAE=∠EAF,根据三角形的角平分线的定义得到AE平分∠DAF;又因为∠BAD=∠CAF,利用等式的性质可得∠BAD+∠DAE=∠CAF+∠EAF,∠BAE=∠EAC,根据三角形的角平分线的定义得到AE平分∠BAC.
解答:解:∵∠DAE=∠EAF,
∴AE平分∠DAF;
又∵∠BAD=∠CAF,
∴∠BAD+∠DAE=∠CAF+∠EAF,即∠BAE=∠EAC,
∴AE平分∠BAC.
故答案为③⑤.
∴AE平分∠DAF;
又∵∠BAD=∠CAF,
∴∠BAD+∠DAE=∠CAF+∠EAF,即∠BAE=∠EAC,
∴AE平分∠BAC.
故答案为③⑤.
点评:本题主要考查了三角形的角平分线的定义:三角形一个角的平分线与这个角的对边交于一点,这个角的顶点与交点间的线段叫做三角形的角平分线.

练习册系列答案
相关题目
 如图,在矩形ABCD中,对角线AC、BD相交于G,E为AD的中点,连接BE交AC于F,连接FD,若∠BFA=90°,则下列四对三角形:①△BEA与△ACD;②△FED与△DEB;③△CFD与△ABG;④△ADF与△EFD,其中相似的为( )
如图,在矩形ABCD中,对角线AC、BD相交于G,E为AD的中点,连接BE交AC于F,连接FD,若∠BFA=90°,则下列四对三角形:①△BEA与△ACD;②△FED与△DEB;③△CFD与△ABG;④△ADF与△EFD,其中相似的为( )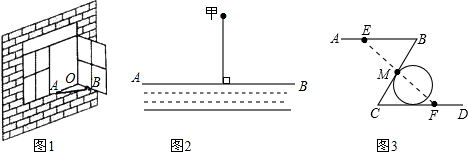
 如图,AB∥CD.如果∠A+∠AMN=180°,那么MN与CD平行吗?说说你的理由.
如图,AB∥CD.如果∠A+∠AMN=180°,那么MN与CD平行吗?说说你的理由.