题目内容
 如图,在矩形ABCD中,对角线AC、BD相交于G,E为AD的中点,连接BE交AC于F,连接FD,若∠BFA=90°,则下列四对三角形:①△BEA与△ACD;②△FED与△DEB;③△CFD与△ABG;④△ADF与△EFD,其中相似的为( )
如图,在矩形ABCD中,对角线AC、BD相交于G,E为AD的中点,连接BE交AC于F,连接FD,若∠BFA=90°,则下列四对三角形:①△BEA与△ACD;②△FED与△DEB;③△CFD与△ABG;④△ADF与△EFD,其中相似的为( )| A、①④ | B、①② |
| C、②③④ | D、①②③④ |
考点:相似三角形的判定
专题:
分析:根据判定三角形相似的条件对选项逐一进行判断.
解答:解:①根据题意得:∠BAE=∠ADC=∠AFE=90°
∴∠AEF+∠EAF=90°,∠DAC+∠ACD=90°
∴∠AEF=∠ACD
∴①中两三角形相似;
②∵∠AEB=∠FEA,∠AFE=∠EAB=90°,
∴△AFE∽△BAE,
∴
=
,
又∵AE=ED,
∴
=
而∠BED=∠BED,
 ∴△FED∽△DEB.
∴△FED∽△DEB.
故②正确;
③∵AB∥CD,
∴∠BAC=∠GCD,
∵∠ABE=∠DAF,∠EBD=∠EDF,且∠ABG=∠ABE+∠EBD,
∴∠ABG=∠DAF+∠EDF=∠DFC;
∵∠ABG=∠DFC,∠BAG=∠DCF,
∴△CFD∽△ABG,故③正确;
④∵△FED∽△DEB,
∴∠EFD=∠EDB,
∵AG=DG,
∴∠DAF=∠ADG,
∴∠DAF=∠EFD,
∴△ADF∽△EFD;
所以相似的有①②③④.
故选:D.
∴∠AEF+∠EAF=90°,∠DAC+∠ACD=90°
∴∠AEF=∠ACD
∴①中两三角形相似;
②∵∠AEB=∠FEA,∠AFE=∠EAB=90°,
∴△AFE∽△BAE,
∴
| AE |
| EF |
| EB |
| AE |
又∵AE=ED,
∴
| ED |
| EF |
| EB |
| ED |
而∠BED=∠BED,
 ∴△FED∽△DEB.
∴△FED∽△DEB.故②正确;
③∵AB∥CD,
∴∠BAC=∠GCD,
∵∠ABE=∠DAF,∠EBD=∠EDF,且∠ABG=∠ABE+∠EBD,
∴∠ABG=∠DAF+∠EDF=∠DFC;
∵∠ABG=∠DFC,∠BAG=∠DCF,
∴△CFD∽△ABG,故③正确;
④∵△FED∽△DEB,
∴∠EFD=∠EDB,
∵AG=DG,
∴∠DAF=∠ADG,
∴∠DAF=∠EFD,
∴△ADF∽△EFD;
所以相似的有①②③④.
故选:D.
点评:此题考查了相似三角形的判定:
①有两个对应角相等的三角形相似;
②有两个对应边的比相等,且其夹角相等,则两个三角形相似;
③三组对应边的比相等,则两个三角形相似.
①有两个对应角相等的三角形相似;
②有两个对应边的比相等,且其夹角相等,则两个三角形相似;
③三组对应边的比相等,则两个三角形相似.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
 如图,一段抛物线:y=-x(x-4)(0≤x≤4),记为C1,它与x轴交于点O,A1;将C2绕点A2;…如此进行下去,得到一条连续的曲线,若P(2013,m)在这条曲线上,则m的值为( )
如图,一段抛物线:y=-x(x-4)(0≤x≤4),记为C1,它与x轴交于点O,A1;将C2绕点A2;…如此进行下去,得到一条连续的曲线,若P(2013,m)在这条曲线上,则m的值为( )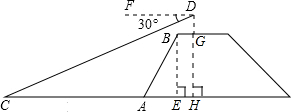 如图,张明站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,他测得小船C的俯角是∠FDC=30°,若张明的眼睛与地面的距离是1.5米,BG=1米,BG平行于AC所在的直线,tan∠BAE=4:3,坡长AB=10米,求小船C到岸边的距离CA的长?(参考数据:根号
如图,张明站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,他测得小船C的俯角是∠FDC=30°,若张明的眼睛与地面的距离是1.5米,BG=1米,BG平行于AC所在的直线,tan∠BAE=4:3,坡长AB=10米,求小船C到岸边的距离CA的长?(参考数据:根号 已知:如图,⊙O的直径AD=2,
已知:如图,⊙O的直径AD=2,
 如图,∠DAE=∠EAF,∠BAD=∠CAF,则下列结论:①AD平分∠BAF;②AF平分∠DAC;③AE平分∠DAF;④AF平分∠EAC;⑤AE平分∠BAC,正确的有
如图,∠DAE=∠EAF,∠BAD=∠CAF,则下列结论:①AD平分∠BAF;②AF平分∠DAC;③AE平分∠DAF;④AF平分∠EAC;⑤AE平分∠BAC,正确的有