题目内容
△ABC的中线AD、BE相交于G,GP∥BC交AC于点P,BC=6,则GP等于 .
考点:三角形的重心
专题:
分析:作出图形,根据三角形的重心到顶点的距离等于到对边中点的距离的2倍可得AG=2DG,然后求出
=
,再根据相似三角形对应边成比例列式计算即可得解.
| AG |
| AD |
| 2 |
| 3 |
解答: 解:如图,∵△ABC的中线AD、BE相交于G,
解:如图,∵△ABC的中线AD、BE相交于G,
∴AG=2DG,
∴
=
,
∵BC=6,AD是中线,
∴CD=
BC=
×6=3,
∵GP∥BC,
∴△AGP∽△ADC,
∴
=
=
,
∴GP=
CD=
×3=2.
故答案为:2.
 解:如图,∵△ABC的中线AD、BE相交于G,
解:如图,∵△ABC的中线AD、BE相交于G,∴AG=2DG,
∴
| AG |
| AD |
| 2 |
| 3 |
∵BC=6,AD是中线,
∴CD=
| 1 |
| 2 |
| 1 |
| 2 |
∵GP∥BC,
∴△AGP∽△ADC,
∴
| GP |
| CD |
| AG |
| AD |
| 2 |
| 3 |
∴GP=
| 2 |
| 3 |
| 2 |
| 3 |
故答案为:2.
点评:本题考查了三角形的重心,相似三角形的判定与性质,熟记三角形的重心到顶点的距离等于到对边中点的距离的2倍是解题的关键,此内容很多教材已经不作要求,此题可斟酌使用.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
下列性质正方形具有而矩形不具有的是( )
| A、四角相等 |
| B、对角线互相垂直 |
| C、对角线相等 |
| D、对角线互相平分 |
已知x2+y2=13,xy=-2,则①(x-y)2=17;②(x+y)2-(x-y)2=8;③x+y=3;④(2x-y)(2y-x)=-36,其中正确的有( )
| A、1 个 |
| B、2 个 |
| C、3 个 |
| D、4 个 |
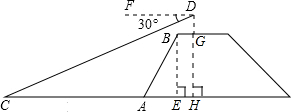 如图,张明站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,他测得小船C的俯角是∠FDC=30°,若张明的眼睛与地面的距离是1.5米,BG=1米,BG平行于AC所在的直线,tan∠BAE=4:3,坡长AB=10米,求小船C到岸边的距离CA的长?(参考数据:根号
如图,张明站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,他测得小船C的俯角是∠FDC=30°,若张明的眼睛与地面的距离是1.5米,BG=1米,BG平行于AC所在的直线,tan∠BAE=4:3,坡长AB=10米,求小船C到岸边的距离CA的长?(参考数据:根号 如图所示,已知点P是△ABC三条角平分线的交点,PD⊥AB,若PD=5,△ABC的周长为20,求△ABC的面积.
如图所示,已知点P是△ABC三条角平分线的交点,PD⊥AB,若PD=5,△ABC的周长为20,求△ABC的面积. 如图,∠DAE=∠EAF,∠BAD=∠CAF,则下列结论:①AD平分∠BAF;②AF平分∠DAC;③AE平分∠DAF;④AF平分∠EAC;⑤AE平分∠BAC,正确的有
如图,∠DAE=∠EAF,∠BAD=∠CAF,则下列结论:①AD平分∠BAF;②AF平分∠DAC;③AE平分∠DAF;④AF平分∠EAC;⑤AE平分∠BAC,正确的有 如图,AB∥DE,若∠B=30°,∠D=140°,则∠C的大小是
如图,AB∥DE,若∠B=30°,∠D=140°,则∠C的大小是 二次函数y=x2+bx+c的图象经过点(4,3),(3,0).
二次函数y=x2+bx+c的图象经过点(4,3),(3,0).