题目内容
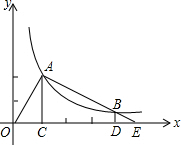 如图,A是反比例函数y=
如图,A是反比例函数y=| k |
| x |
考点:反比例函数综合题
专题:
分析:首先求得A和B的坐标,然后利用待定系数法求得OA和AB的解析式,然后根据AB⊥OA,则两个函数的解析式的一次项系数的乘积是-1,即可求得k的值.
解答:解:把x=1代入y=
得:y=k,则A的坐标是(1,k),
同理B的坐标是(4,
),
则直线OA的解析式是y=kx,
设直线AB的解析式是y=mx+n,
则
,
解得:
.
则直线AB的解析式是y=-
kx+
k,
∵AB⊥OA,
∴k•(-
k)=-1,
解得:k=2或-2(舍去).
故答案是:2.
| k |
| x |
同理B的坐标是(4,
| k |
| 4 |
则直线OA的解析式是y=kx,
设直线AB的解析式是y=mx+n,
则
|
解得:
|
则直线AB的解析式是y=-
| 1 |
| 4 |
| 5 |
| 4 |
∵AB⊥OA,
∴k•(-
| 1 |
| 4 |
解得:k=2或-2(舍去).
故答案是:2.
点评:本题是一次函数与反比例函数的综合题,主要考查了待定系数法求函数的解析式,理解AB⊥OA的条件是关键.

练习册系列答案
相关题目
在△ABC中,AB=AC=13,BC=10,则△ABC的面积为( )
| A、30 | B、60 | C、65 | D、120 |
 如图,直角坐标系内的梯形AOBC,AC∥OB,AC、OB的长分别是关于x的方程x2-6mx+m2+4=0的两根,并且S△AOC:S△BOC=1:5.
如图,直角坐标系内的梯形AOBC,AC∥OB,AC、OB的长分别是关于x的方程x2-6mx+m2+4=0的两根,并且S△AOC:S△BOC=1:5. 平行四边形ABCD中,过A作AE⊥BC,垂足为E,连DE、F为线段DE上一点,且∠1=∠B.求证:△ADF∽△DEC.
平行四边形ABCD中,过A作AE⊥BC,垂足为E,连DE、F为线段DE上一点,且∠1=∠B.求证:△ADF∽△DEC.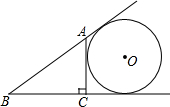 如图,AC⊥BC于点C,⊙O与直线AB、BC、CA都相切,若⊙O的半径等于1,BC=2,△ABC的周长是
如图,AC⊥BC于点C,⊙O与直线AB、BC、CA都相切,若⊙O的半径等于1,BC=2,△ABC的周长是 如图,为了测量某建筑物的高AB,在距离点B25米的D处安置测角仪,测得点A的仰角α为71°6′,已知仪器的高CD=1.52米,求建筑物的高AB.
如图,为了测量某建筑物的高AB,在距离点B25米的D处安置测角仪,测得点A的仰角α为71°6′,已知仪器的高CD=1.52米,求建筑物的高AB.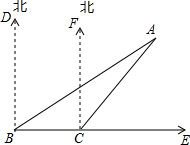 如图,一艘渔船在B处测得灯塔A在北偏东60°的方向,另一艘货轮在C处测得灯塔A在北偏东40°的方向,那么在灯塔A处观看B和C时的视角∠BAC是多少度?
如图,一艘渔船在B处测得灯塔A在北偏东60°的方向,另一艘货轮在C处测得灯塔A在北偏东40°的方向,那么在灯塔A处观看B和C时的视角∠BAC是多少度? 已知:如图,CB⊥BE于B,ED⊥CD于D,BE、CD交于点A,并且AB=AD,求证:△ABC≌△ADE.
已知:如图,CB⊥BE于B,ED⊥CD于D,BE、CD交于点A,并且AB=AD,求证:△ABC≌△ADE.