题目内容
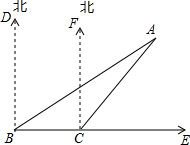 如图,一艘渔船在B处测得灯塔A在北偏东60°的方向,另一艘货轮在C处测得灯塔A在北偏东40°的方向,那么在灯塔A处观看B和C时的视角∠BAC是多少度?
如图,一艘渔船在B处测得灯塔A在北偏东60°的方向,另一艘货轮在C处测得灯塔A在北偏东40°的方向,那么在灯塔A处观看B和C时的视角∠BAC是多少度?考点:方向角
专题:
分析:根据方向角,可得∠DBA=60°,∠FCA=40°,根据角的和差,可得∠ABC,∠ACB的度数,根据三角形的内角和定理,可得答案.
解答:解:由题意,得∠DBA=60°,∠FCA=40°.
由角的和差,得∠ABC=∠DBC-∠DBA=90°-60°=30°,
∠ACB=∠BCF+∠FCA=90°+40°=130°.
由三角形的内角和定理,得
∠BAC=180°-∠ABC-∠BCA
=180°-30°-130°
=20°.
答:在灯塔A处观看B和C时的视角∠BAC是20°.
由角的和差,得∠ABC=∠DBC-∠DBA=90°-60°=30°,
∠ACB=∠BCF+∠FCA=90°+40°=130°.
由三角形的内角和定理,得
∠BAC=180°-∠ABC-∠BCA
=180°-30°-130°
=20°.
答:在灯塔A处观看B和C时的视角∠BAC是20°.
点评:本题考查了方向角,利用了方向角,角的和差,三角形的内角和定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
计算:2cos60°+2sin30°+4tan45°=( )
A、2+2
| ||
B、5+
| ||
| C、6 | ||
D、4
|
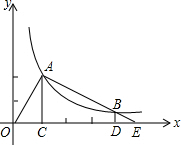 如图,A是反比例函数y=
如图,A是反比例函数y=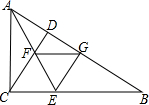 如图,在△ABC中,∠ACB=90°,CD⊥AB,AE平分∠BAC交CD于F,EG⊥AB于G,求证:四边形CEGF是菱形.
如图,在△ABC中,∠ACB=90°,CD⊥AB,AE平分∠BAC交CD于F,EG⊥AB于G,求证:四边形CEGF是菱形.
 已知点P为⊙O所在平面上一点,过点P的两条直线PA,PC分别交⊙O于A,B和C,D两点,且PO平分∠APC.求证:PA=PC.
已知点P为⊙O所在平面上一点,过点P的两条直线PA,PC分别交⊙O于A,B和C,D两点,且PO平分∠APC.求证:PA=PC.