题目内容
如图，直角坐标系内的梯形AOBC，AC∥OB，AC、OB的长分别是关于x的方程x2-6mx+m2+4=0的两根，并且S△AOC：S△BOC=1：5．（1）求AC、OB的长；
（2）当BC⊥OC时，求OC的长及OC所在的直线解析式．
考点：一次函数综合题
专题：综合题
分析：（1）根据等高三角形的面积等于底边比，可得出AC：OB=1：5，根据韦达定理得出AC、OB的和与积的值，然后联立AC、OB的比例关系式可求出AC、OB的长；
（2）本题要通过相似三角形求解，先得出△ACO∽△COB，根据相似三角形得出的OC2=AC•OB，可求出OC的长，进而可在直角三角形OAC中，求出OA的长，继而可得出点C的坐标，用待定系数法可求出OC所在直线的解析式；
（2）本题要通过相似三角形求解，先得出△ACO∽△COB，根据相似三角形得出的OC2=AC•OB，可求出OC的长，进而可在直角三角形OAC中，求出OA的长，继而可得出点C的坐标，用待定系数法可求出OC所在直线的解析式；
解答：解：（1）∵AC、OB的长分别是关于x的方程x2-6mx+m2+4=0的两根，
∴AC+OB=6m，AC•OB=m2+4，
又∵S△AOC：S△BOC=1：5，
∴AC：0B=1：5，
综上可得：
，
解得：
．
即AC长为1，OB长为5．
（2）由题意得：BC⊥OC，则∠BC0=90°，
∵∠OCA=∠BOC（同角的余角相等），∠OAC=∠BC0=90°，
∴△ACO∽△COB，
∴
=
，
∴CO2=5，
在Rt△AOC中，OA=
=2，
∴点C的坐标为（1，2），
设直线OC所在的直线解析式为y=kx，
将点C的坐标代入可得：2=k，
直线OC所在的直线解析式为y=2x．
∴AC+OB=6m，AC•OB=m2+4，
又∵S△AOC：S△BOC=1：5，
∴AC：0B=1：5，
综上可得：
|
解得：
|
即AC长为1，OB长为5．
（2）由题意得：BC⊥OC，则∠BC0=90°，
∵∠OCA=∠BOC（同角的余角相等），∠OAC=∠BC0=90°，
∴△ACO∽△COB，
∴
| AC |
| CO |
| CO |
| OB |
∴CO2=5，
在Rt△AOC中，OA=
| OC2-AC2 |
∴点C的坐标为（1，2），
设直线OC所在的直线解析式为y=kx，
将点C的坐标代入可得：2=k，
直线OC所在的直线解析式为y=2x．
点评：本题考查了一次函数的综合，涉及了待定系数法求一次函数解析式、勾股定理及一元二次方程的根，解答本题的关键是求出AC、OB的长度，有一定难度．
练习册系列答案
相关题目
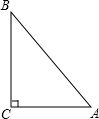已知：如图，Rt△ABC中，∠C=90°，AC=6，AB=10．
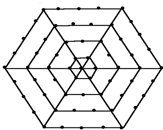如图，有一个形如六边形的点阵，它的中心是一个点，算第一层，第二层每边有两个点，第三层每边有三个点，依此类推．
如图，A、B两点在数轴上对应的数分别是-20、24，点P、Q两点同时出发，在数轴上运动，它们的速度分别是2个单位/秒、4个单位/秒，它们运动的时间为t秒，当点P、Q在A、B之间相向运动，且满足OP=OQ，则点P对应的数是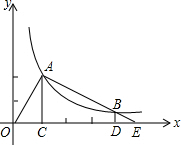
如图，A是反比例函数y=