题目内容
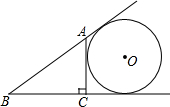 如图,AC⊥BC于点C,⊙O与直线AB、BC、CA都相切,若⊙O的半径等于1,BC=2,△ABC的周长是
如图,AC⊥BC于点C,⊙O与直线AB、BC、CA都相切,若⊙O的半径等于1,BC=2,△ABC的周长是考点:切线的性质
专题:
分析:设BA、BC、AC与⊙O的切点分别为D、E、F,连接OE、OF,由切线的性质可得OE⊥BE、OF⊥AC,则可得四边形CEOF为正方形,可得CF=CE=OF=1,则BE=1+2=3,又由切线长定理可得BD=BE=3,AF=AD,所以可求得△ABC的周长为BD+BE=2BD=6.
解答: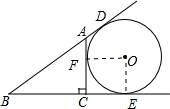 解:设BA、BC、AC与⊙O的切点分别为D、E、F,连接OE、OF,如图,
解:设BA、BC、AC与⊙O的切点分别为D、E、F,连接OE、OF,如图,
∵AC、BE为切线,
∴OE⊥BE、OF⊥AC,且AC⊥BC,OE=OF=1,
∴四边形CEOF为正方形,
∴CE=CF=1,
又由切线长定理,可知BD=BE,AD=AF,
∴△ABC的周长为:BA+BC+AC=BA+AF+BC+CF=BA+AD+BC+CE=BD+BE=2BE=2(BC+CE)=2(2+1)=6,
故答案为:6.
 解:设BA、BC、AC与⊙O的切点分别为D、E、F,连接OE、OF,如图,
解:设BA、BC、AC与⊙O的切点分别为D、E、F,连接OE、OF,如图,∵AC、BE为切线,
∴OE⊥BE、OF⊥AC,且AC⊥BC,OE=OF=1,
∴四边形CEOF为正方形,
∴CE=CF=1,
又由切线长定理,可知BD=BE,AD=AF,
∴△ABC的周长为:BA+BC+AC=BA+AF+BC+CF=BA+AD+BC+CE=BD+BE=2BE=2(BC+CE)=2(2+1)=6,
故答案为:6.
点评:本题主要考查切线的性质及切线长定理,由条件求得BE=BD,且求得BE=3是解题的关键.已知切点时,连接圆心和切点是常用的辅助线.

练习册系列答案
相关题目
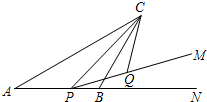 如图,△ABC中,AC=10,∠BAC=30°,点P是射线AB上的一个动点,cos∠CPM=
如图,△ABC中,AC=10,∠BAC=30°,点P是射线AB上的一个动点,cos∠CPM= 如图,A是反比例函数y=
如图,A是反比例函数y= 如图,直角梯形ABCD中,AD=3,AB=11,BC=6,AB⊥BC,动点P在线段AB上运动,如果满足△ADP和△BCP相似,计算此时线段AP的长度.
如图,直角梯形ABCD中,AD=3,AB=11,BC=6,AB⊥BC,动点P在线段AB上运动,如果满足△ADP和△BCP相似,计算此时线段AP的长度.