题目内容
 平行四边形ABCD中,过A作AE⊥BC,垂足为E,连DE、F为线段DE上一点,且∠1=∠B.求证:△ADF∽△DEC.
平行四边形ABCD中,过A作AE⊥BC,垂足为E,连DE、F为线段DE上一点,且∠1=∠B.求证:△ADF∽△DEC.考点:相似三角形的判定,平行四边形的性质
专题:证明题
分析:先根据平行线的性质得出∠ADF=∠DEC,∠C+∠B=180°,再根据∠1=∠B,∠1+∠AFD=180°可得出∠C=∠AFD,由此可得出结论.
解答:证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠ADF=∠DEC,∠C+∠B=180°.
∵∠1=∠B,∠1+∠AFD=180°,
∴∠C=∠AFD,
∴△ADF∽△DEC.
∴AD∥BC,AB∥CD,
∴∠ADF=∠DEC,∠C+∠B=180°.
∵∠1=∠B,∠1+∠AFD=180°,
∴∠C=∠AFD,
∴△ADF∽△DEC.
点评:本题考查的是相似三角形的判定定理,熟知有两组角对应相等的两个三角形相似是解答此题的关键.

练习册系列答案
相关题目
把代数式“
-5”用文字语言叙述,其中表述不正确的是( )
| 1 |
| x |
| A、比x的倒数小5的数 |
| B、x的倒数与5的差 |
| C、x与5的差的倒数 |
| D、1除以x的商与5的差 |
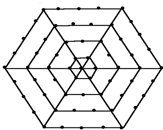 如图,有一个形如六边形的点阵,它的中心是一个点,算第一层,第二层每边有两个点,第三层每边有三个点,依此类推.
如图,有一个形如六边形的点阵,它的中心是一个点,算第一层,第二层每边有两个点,第三层每边有三个点,依此类推. 如图,A、B两点在数轴上对应的数分别是-20、24,点P、Q两点同时出发,在数轴上运动,它们的速度分别是2个单位/秒、4个单位/秒,它们运动的时间为t秒,当点P、Q在A、B之间相向运动,且满足OP=OQ,则点P对应的数是
如图,A、B两点在数轴上对应的数分别是-20、24,点P、Q两点同时出发,在数轴上运动,它们的速度分别是2个单位/秒、4个单位/秒,它们运动的时间为t秒,当点P、Q在A、B之间相向运动,且满足OP=OQ,则点P对应的数是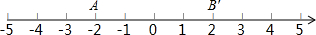
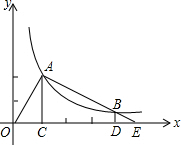 如图,A是反比例函数y=
如图,A是反比例函数y= 延长线段AB是指按从端点A到B的方向延长;延长线段BA是指按从端点B到A的方向延长,这时也可以说成反向延长线段AB,如图,分别画出线段AB的延长线和反向延长线.
延长线段AB是指按从端点A到B的方向延长;延长线段BA是指按从端点B到A的方向延长,这时也可以说成反向延长线段AB,如图,分别画出线段AB的延长线和反向延长线.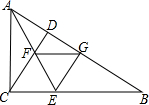 如图,在△ABC中,∠ACB=90°,CD⊥AB,AE平分∠BAC交CD于F,EG⊥AB于G,求证:四边形CEGF是菱形.
如图,在△ABC中,∠ACB=90°,CD⊥AB,AE平分∠BAC交CD于F,EG⊥AB于G,求证:四边形CEGF是菱形.